Hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 3 Bài 1 Hàm số và đồ thị giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Câu hỏi khởi động trang 31 SGK Toán 10 Cánh diều tập 1 - CD
Galileo Galilei (1564 - 1642). sinh tại thành phố Pisa (Italia). là nhà bác học vī đại của thời kì Phục Hưng. Ông được mệnh danh là “cha đẻ của khoa học hiện đại”. Trước Galileo. người ta tin rằng vật nặng rơi nhanh hơn vật nhẹ, ông đã bác bỏ điểu này bằng thí nghiệm nổi tiếng ở tháp nghiêng Pisa. Từ thí nghiệm của Galileo, các nhà khoa học sau này được truyển cảm hứng rằng chúng ta chỉ có thể rút ra tri thúc khoa học từ các quy luật khách quan của tự nhiên, chứ không phải từ niềm tin.
Làm thế nào để mô tả được mối liên hệ giữa thời gian t và quãng đuờmg đi đuợc S của vật rơi tự do? Làm thế nào để có được hình ảnh hình học mình hoạ mối liên hệ giữa hai đại lượng đó?
-
Hoạt động 1 trang 31 SGK Toán 10 Cánh diều tập 1 - CD
Trong bài toán ở phần mở đầu, ta đã biết công thức tính quãng đường đi được \(S\left( m \right)\) của vật rơi tự do theo thời gian \(t\left( s \right)\) là: \(S = \frac{1}{2}g{t^2}\), trong đó \(g\) là gia tốc rơi tự do, \(g \approx 9,8\left( {m/{s^2}} \right)\).
a) Với mỗi giá trị \(t = 1,t = 2\), tính giá trị tương ứng của S.
b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của S?
-
Hoạt động 2 trang 31 SGK Toán 10 Cánh diều tập 1 - CD
Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức sau: \(y = - 200{x^2} + 92{\rm{ }}000x - 8{\rm{ }}400{\rm{ }}000\), trong đó x là số sản phẩm loại đó được bán ra.
a) Với mỗi giá trị x = 100, x = 200, tính giá trị tương ứng của y.
b) Với mỗi giá trị của x có bao nhiêu giá trị tương ứng của y?
-
Luyện tập 1 trang 32 SGK Toán 10 Cánh diều tập 1 - CD
Trong y học, một người cân nặng 60 kg chạy với tốc độ 6,5 km/h thì lượng ca-lo tiêu thụ được tính theo công thức: c=4,7t (Nguồn: https://irace.vn).
Trong đó thời gian t được tính theo phút. Hỏi c có phải là hàm số của t không? Vì sao?
-
Hoạt động 3 trang 32 SGK Toán 10 Cánh diều tập 1 - CD
Cho hai hàm số \(y = 2x + 1\left( 1 \right)\) và \(y = \sqrt {x - 2} \left( 2 \right)\)
a) Nêu biểu thức xác định mỗi hàm số trên.
b) Tìm x sao cho mỗi biểu thức trên có nghĩa.
-
Luyện tập 2 trang 32 SGK Toán 10 Cánh diều tập 1 - CD
Tìm tập xác định của hàm số: \(y = \frac{{\sqrt {x + 2} }}{{x - 3}}\)
-
Luyện tập 3 trang 33 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số: \(y = \left\{ \begin{array}{l} - x\,{\rm{ nếu} \, x < 0}\\{ x\, \rm{nếu} \, x > 0}\end{array} \right.\)
a) Tìm tập xác định của hàm số trên.
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
-
Hoạt động 4 trang 34 SGK Toán 10 Cánh diều tập 1 - CD
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = - 1;{x_2} = 1\).
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
-
Luyện tập 4 trang 34 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
-
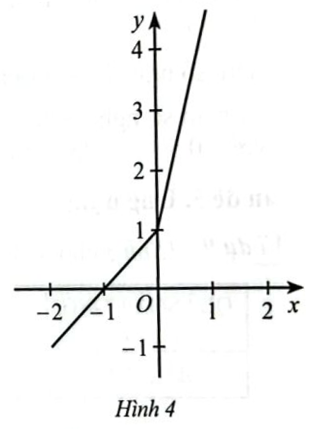
Luyện tập 5 trang 35 SGK Toán 10 Cánh diều tập 1 - CD
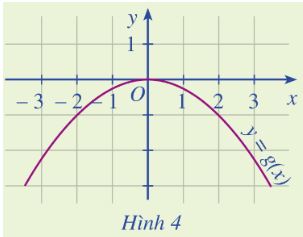
Dựa vào Hình 4, xác định \(g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)\).
-
Hoạt động 5 trang 36 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(f\left( x \right) = x + 1\).
a) So sánh \(f\left( 1 \right)\) và \(f\left( 2 \right)\).
b) Chứng minh rằng nếu \({x_1},{x_2} \in \mathbb{R}\) sao cho \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
-
Luyện tập 6 trang 36 SGK Toán 10 Cánh diều tập 1 - CD
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
-
Hoạt động 6 trang 36 SGK Toán 10 Cánh diều tập 1 - CD
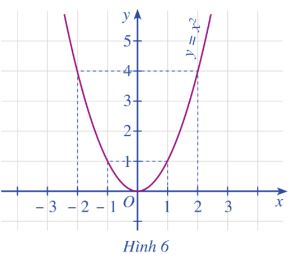
Cho đồ thị hàm số \(y = f\left( x \right) = {x^2}\) như Hình 6.
a) So sánh \(f\left( { - 2} \right),f\left( { - 1} \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.
b) So sánh \(f\left( 1 \right),f\left( 2 \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
-
Giải bài 1 trang 37 SGK Toán 10 Cánh diều tập 1 - CD
Tìm tập xác định của mỗi hàm số sau:
a) \(y = - {x^2}\)
b) \(y = \sqrt {2 - 3x} \)
c) \(y = \frac{4}{{x + 1}}\)
d) \(y = \left\{ \begin{array}{l}1{\rm{ khi }}x \in \mathbb{Q}\\0{\rm{ khi }}x \in \mathbb{R}\backslash \mathbb{Q}\end{array} \right.\)
-
Giải bài 2 trang 37 SGK Toán 10 Cánh diều tập 1 - CD
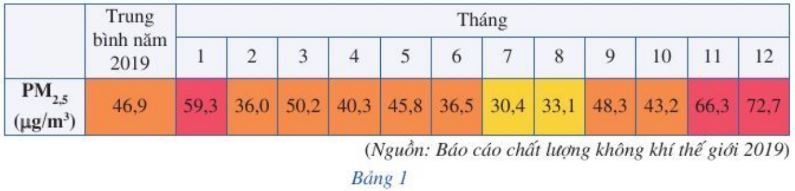
Bảng 1 dưới đây cho biết chỉ số \(P{M_{2,5}}\) (bụi mịn) ở thành phố Hà Nội từ tháng 1 đến tháng 12 của năm 2019.
(Nguồn: Báo cáo chất lượng không khí thế giới 2019)
a) Nêu chỉ số \(P{M_{2,5}}\) trong tháng 2; tháng 5; tháng 10.
b) Chỉ số \(P{M_{2,5}}\) có phải là hàm số của tháng không? Tại sao?
-
Giải bài 3 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
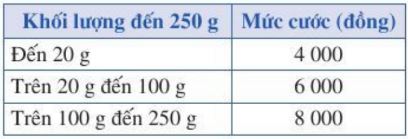
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có không lượng đến 250g như trong bảng sau:
a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x(g) hay không? Nếu đúng, hãy xác định những công thức tính y.
b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g.
-
Giải bài 4 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = - 2{x^2}\).
a) Điểm nào trong các điểm có tọa độ \(\left( { - 1; - 2} \right),\left( {0;0} \right),\left( {0;1} \right),\left( {2021;1} \right)\) thuộc đồ thị của hàm số trên?
b) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng \( - 2;3\) và 10.
c) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng \( - 18\).
-
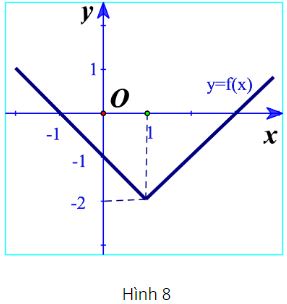
Giải bài 5 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
-
Giải bài 6 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = \frac{1}{x}\). Chứng tỏ hàm số đã cho:
a) Nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
b) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
-
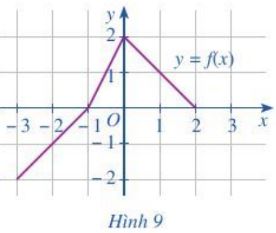
Giải bài 7 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
-
Giải bài 8 trang 38 SGK Toán 10 Cánh diều tập 1 - CD
Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.
Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe.
Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất?
-
Giải bài 1 trang 42 SBT Toán 10 Cánh diều tập 1 - CD
Trong các công thức sau, công thức nào không biểu diễn \(y\) là hàm số của \(x\)?
A. \(x + 2y = 3\)
B. \(y = \sqrt {{x^2} - 2x} \)
C. \(y = \frac{1}{x}\)
D. \({x^2} + {y^2} = 4\)
-
Giải bài 2 trang 42 SBT Toán 10 Cánh diều tập 1 - CD
Cho đồ thị hàm số \(y = f\left( x \right)\) ở Hình 4. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số cắt trục hoành tại điểm của hoành độ bằng 1
B. Đồ thị hàm số cắt trục tung tại điểm có tung bộ bằng -1
C. Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\), ngịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\)
D. Hàm số đồng biến trên \(\mathbb{R}\)
-
Giải bài 3 trang 42 SBT Toán 10 Cánh diều tập 1 - CD
Tìm tập xác định của mỗi hàm số sau:
a) \(y = - {x^3} + 4x - 1\)
b) \(y = \sqrt {5 - 6x} \)
c) \(y = \frac{4}{{3x + 1}}\)
d) \(y = \frac{1}{{2x - 1}} - \sqrt {3 - x} \)
e) \(y = \frac{{2x + 3}}{{{x^2} + 3x - 4}}\)
g) \(y = \left\{ \begin{array}{l}x - 1,x > 0\\5x + 1,x < - 1\end{array} \right.\)
-
Giải bài 4 trang 42 SBT Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = \left\{ \begin{array}{l} - x + 1,x < 0\\0,x = 0\\1,x > 0\end{array} \right.\)
a) Tìm tập xác định của hàm số trên
b) Tính giá trị của hàm số khi \(x = - 2,x = 0,x = 2021\)
-
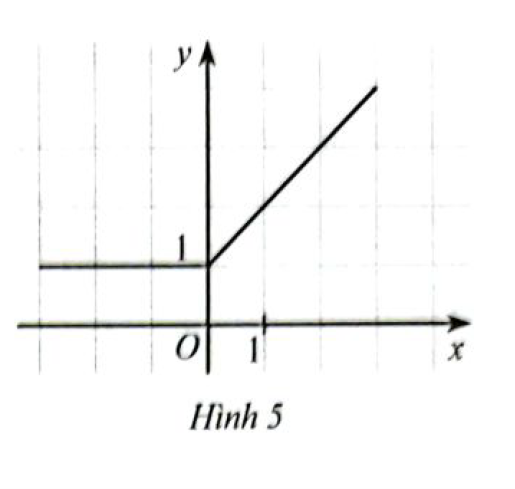
Giải bài 5 trang 43 SBT Toán 10 Cánh diều tập 1 - CD
Quan sát đồ thị hàm số \(y = f\left( x \right)\) ở Hình 5
a) Trong các điểm có tọa độ (1;2), (0;0). (2;3) điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right),f\left( 3 \right)\)
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 1
-
Giải bài 6 trang 43 SBT Toán 10 Cánh diều tập 1 - CD
Cho bảng biến thiên hàm số \(y = f\left( x \right)\) như sau:

a) Tìm khoảng đồng biến, ngịch biến của hàm số \(y = f\left( x \right)\)
b) So sánh \(f\left( { - 2021} \right)\) và \(f\left( { - 1} \right)\); \(f\left( {\sqrt 3 } \right)\) và \(f\left( 2 \right)\)
-
Giải bài 7 trang 43 SBT Toán 10 Cánh diều tập 1 - CD
Cho hàm số \(y = \frac{{ - 2}}{x}\). Chứng tỏ hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\)
-
Giải bài 8 trang 43 SBT Toán 10 Cánh diều tập 1 - CD
Một nhân viên bán hàng sẽ nhận được một mức lương cơ bản là 5 triệu đồng mỗi tháng và một khoản hoa hồng là 5% nếu tổng doanh thu trên 10 triệu đồng trong tháng. Ngoài ra, nếu doanh số bán hàng hàng tháng là 20 triệu đồng hoặc nhiều hơn thì nhân viên bán hàng nhận được thêm tiền thưởng là 500 nghìn đồng
a) Hãy biểu diễn thu nhập hàng tháng của nhân viên đó bằng một hàm số theo doanh số bán hàng
b) Nếu doanh số trong 1 tháng của nhân viên đó là 30 triệu đồng thì nhân viên đó sẽ nhận được bao nhiêu tiền lương?