Sau đây mời các em học sinh lớp cùng tìm hiểu về bài Tập hợp, các phép toán trên tập hợp. Bài giảng đã được soạn khái quát lý thuyết cần nhớ, đồng thời có các bài tập minh họa có lời giải chi tiết giúp các em dễ dàng nắm được kiến thức trọng tâm của bài.
Tóm tắt lý thuyết
1.1. Tập hợp
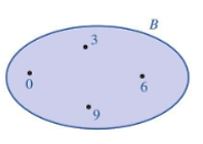
Ví dụ: Cho tập hợp B gồm các số tự nhiên có một chữ số và chi hết cho 3.
a) Viết tập hợp B theo hai cách: liệt kê các phần tử của tập hợp; chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
b) Minh hoạ tạp hợp B bằng biểu đồ ven.
Giải
a) Tập hợp B được viết theo cách liệt kê các phần tử là: B = {0; 3; 6; 9}.
Tập hợp B được viết theo cách chỉ ra tính chất đặc trưng cho các phần tử là: \(B = {\rm{\{ }}x \in N|x \le 9\) và \(x \vdots 3\} \)
b) Tập hợp B được minh hoạ bằng biểu đồ Ven ở hình sau
Nhận xét
- Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (tập rỗng), kí hiệu là \(\emptyset \).
- Một tập hợp có thể không có phần tử nào, cũng có thể có một phần tử, có nhiều phần tử, có vô số phần tử.
Chú ý: Khi tập hợp C là tập hợp rỗng, ta viết \(C = \emptyset \) và không được viết là \(C = \left\{ \emptyset \right\}\).
1.2. Tập con và tập hợp bằng nhau
a) Tập con
| Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của B và viết là \(A \subset B\). Ta còn đọc là A chứa trong B. |
|---|
Qui ước: Tập hợp rỗng \(\emptyset \) được coi là tập con của mọi tập hợp.
Chú ý: \(A \subset B \Leftrightarrow \left( {\forall x,x \in A \Rightarrow x \in B} \right).\)
Khi \(A \subset B\), ta cũng viết \(B \supset A\) (đọc là B chứa A)
Nếu A không phải là tập con của B, ta viết \(A \not\subset B\).
Ví dụ: Cho hai tập hợp: \(E = \left\{ {x \in R|x \le 1} \right\},F = \left\{ {x \in R|x < 2} \right\}\). Chứng tỏ rằng \(E \subset F\).
Giải
Lấy phần tử x tùy ý thuốc E. Ta có: \(x \le 1\). Vì \(x \le 1\) nên x < 2. Do đó \(x \in F\).
Vậy \(E \subset F\).
|
Ta có các tính chất sau:
|
|---|
b) Tập hợp bằng nhau
| Khi \(A \subset B\) và \(B \subset A\) thì ta nói hai tập hợp A và B bằng nhau, viết là A = B. |
|---|
Chú ý: \(A = B \Leftrightarrow \left( {\forall x,x \in A \Leftrightarrow x \in B} \right)\).
Ví dụ: Cho C là tập hợp các tam giác có ba cạnh bằng nhau và D là tập hợp các tam giác có ba góc bằng nhau. Hai tập hợp C và D có bằng nhau hay không?
Giải
Do một tam giác có ba cạnh bằng nhau khi và chỉ khi tam giác đó có ba góc bằng nhau nên hai tập hợp C và D là bằng nhau.
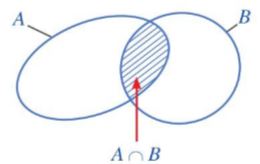
1.3. Giao của hai tập hợp
| Tập hợp gồm tất cả các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B được gọi là giao của hai tập hợp A và B, kí hiệu \(A \cap B\). |
|---|
Vậy \(A \cap B = {\rm{\{ x|x}} \in {\rm{A}}\) và \(x \in {\rm{B\} }}\)
Tập hợp \(A \cap B\) được minh họa bởi phần gạch chéo trong hình sau
Lưu ý: \(x \in A \cap B\) khi và chỉ khi \(x \in A\) và \(x \in B\)
Ví dụ: Tìm giao của hai tập hợp trong mỗi trường hợp sau:
a) A = {x \(\in\) N | x là ước của 16}, B = {x \(\in\) N | x là ước của 20}
b) C = {x \(\in\) N | x là bội của 4}, D = {x \(\in\) N | x là bội của 5}
Giải
a) A = {1; 2; 4; 8; 16}, B = {1; 2; 4; 5; 10; 20}. Vậy \(A \cap B = \left\{ {1;2;4} \right\}\)
Chú ý: A là tập hợp các ước tự nhiên của 16, B là tâp hợp các ước tự nhiên của 20 nên \(A \cap B\) là tập hợp các ước chung tự nhiên của 16 và 20.
b) \(C \cap D\) = {x \(\in\) N | x là bội của 4 và x là bội của 5}
= {x \(\in\) N | x là bội chung của 4 và 5}
1.4. Hợp của hai tập hợp
| Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B được gọi là hợp của hai tập hợp A và B, kí hiệu \(A \cup B\) |
|---|
Vậy \(A \cup B\) = {x | x \(\in\) A hoặc x \(\in\) B}.
Tập hợp \(A \cup B\) được minh họa bởi phần gạch chéo trong hình sau
Lưu ý: \(x \in A \cup B\) khi và chỉ khi \(x \in A\) hoặc \(x \in B\)
Ví dụ: Cho tập hợp Q các số hữu tỉ và tập hợp I các số vô tỉ. Tìm \(Q \cap I,Q \cup I\)
Giải
Ta có: \(Q \cap I = \emptyset ,Q \cup I = R\)
1.5. Phần bù. Hiệu của hai tập hợp
- Cho tập hợp A là tập con của tập hợp B. Tập hợp những phần tử thuộc B mà không thuộc A được gọi là phần bù của A trong B, kí hiệu \({C_B}A\)
- Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B, kí hiệu A\B.
Vậy \(A\backslash B\) = {x | x \(\in\) A và x \(\notin\) B}.
Tập hợp \(A\backslash B\) được minh họa bởi phần gạch chéo trong hình sau
Ví dụ: Tìm \(A \cap B,A \cup B,A\backslash B,B\backslash A\).
Giải
Ta có: \(A = \left\{ {0;1;2;3} \right\},B = \left\{ 1 \right\}\)
Vậy \(A \cap B = \left\{ 1 \right\},A \cup B = \left\{ {0;1;2;3} \right\},A\backslash B = \left\{ {0;2;3} \right\},B\backslash A = \emptyset \)
1.6. Các tập hợp số
a) Các tập hợp số đã học
Ta đã biết N, Z, Q, R lần lượt là tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực.
Ta có quan hệ sau: \(N \subset Z \subset Q \subset R\)
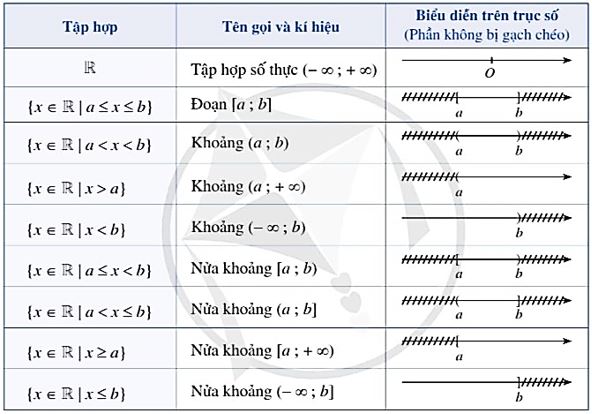
b) Một số tập con thường dùng của tập hợp số thực
Cho a và b là hai số thực với a < b.
Kí hiệu \( - \infty \) đọc là âm vô cực, kí hiệu \( + \infty \) đọc là dương vô cực; a và b được gọi là đầu mút của các đoạn, khoảng, nửa khoảng.
Chú ý: Ta có thể biểu diễn tập hợp trên trục số bằng cách tô màu phần thuộc tập đó, chẳng hạn đoạn [a; b] có thể biểu diễn ở phần tô màu đỏ như hình sau:
Bài tập minh họa
Câu 1: Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
Hướng dẫn giải
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Câu 2: Cho hai tập hợp:
\(A = \{ n \in N|n\)chia hết cho 3},
\(B = \{ n \in N|n\)chia hết cho 9}.
Chứng tỏ rằng \(B \subset A.\)
Hướng dẫn giải
Lấy n bất kì thuộc tập hợp B.
Ta có: n chia hết cho 9 \( \Rightarrow n = 9k\;\;(k \in \mathbb{N})\)
\( \Rightarrow n = 3.(3k)\;\; \vdots \;3\;\;(k \in \mathbb{N})\)
\( \Rightarrow n \in A\)
Như vậy, mọi phần tử của tập hợp B đều là phần tử của tập hợp A hay \(B \subset A.\)
Câu 3: Cho hai tập hợp:
\(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\}\)
\(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} \)
Tìm \(A\,{\rm{\backslash }}\,B\) và \(B\,{\rm{\backslash }}\,A\).
Hướng dẫn giải
Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{ - 2; - 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} = \{ - 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ - 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)
Luyện tập Bài 2 Chương 1 Toán 10 CD
Qua bài giảng trên, giúp các em học sinh:
- Hiểu được khái niệm tập hợp, tập con, hai tập hợp bằng nhau.
- Hiểu được các phép toán giao, hợp của hai tập hợp, hiệu của hai tập hợp, phần bù của một tập con.
3.1. Bài tập trắc nghiệm Bài 2 Chương 1 Toán 10 CD
Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 10 Cánh Diều Chương 1 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. 32
- B. 34
- C. 36
- D. 9
-
- A. 15
- B. 16
- C. 17
- D. 18
-
- A. X = {2; 3}
- B. X = {1; 2; 3; 4}
- C. X = {2; 3; 4}
- D. X = {2; 3; 4; a}
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 2 Chương 1 Toán 10 CD
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 1 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động 1 trang 12 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 1 trang 12 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 3 trang 12 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 1 trang 13 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 4 trang 13 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 2 trang 13 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 5 trang 14 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 3 trang 14 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 6 trang 14 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 7 trang 15 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 4 trang 15 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 8 trang 15 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 9 trang 16 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 5 trang 16 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 1 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 2 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 3 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 4 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 5 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 6 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 7 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 8 trang 18 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 18 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 19 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 20 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 21 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 22 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 23 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 24 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 25 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 26 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 27 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 28 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 29 trang 14 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 30 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 31 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 32 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 33 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 34 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 35 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 36 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 37 trang 15 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 38 trang 16 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 39 trang 16 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 40 trang 16 SBT Toán 10 Cánh diều tập 1 - CD
Hỏi đáp Bài 2 Chương 1 Toán 10 CD
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 10 HỌC247


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)