Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 127390
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau
.png)
Đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\) có bao nhiêu điểm cực trị?
- A. 2
- B. 4
- C. 5
- D. 3
-
Câu 2: Mã câu hỏi: 127582
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
- A. \(y = - {x^3} - 2{x^2} + 3.\)
- B. \(y = \frac{{x + 1}}{{x - 2}}.\)
- C. \(y = \frac{{2x + 1}}{{x + 2}}.\)
- D. \(y = 2{x^3} + 3{x^2} + 10x - 1.\)
-
Câu 3: Mã câu hỏi: 127584
Đường cong hình bên là đồ thị của hàm số \(y = \frac{{{\rm{ax}} + b}}{{cx + d}}\), với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
.png)
- A. \(y' > 0,\forall x \in R\)
- B. \(y' > 0\,\,;\,\,\forall x \ne 1\).
- C. \(y' < 0\,\,;\,\,\forall x \in R.\)
- D. \(y' < 0\,\,;\,\,\forall x \ne 1\).
-
Câu 4: Mã câu hỏi: 127586
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
.png)
- A. \(a < 0,b > 0,c < 0.\)
- B. \(a > 0,b < 0,c > 0\).
- C. \(a > 0,b < 0,c < 0\).
- D. \(a > 0,b > 0,c < 0\).
-
Câu 5: Mã câu hỏi: 127588
Cho hàm số \(y=f(x)\) xác định và liên tục trên R và bảng biến thiên sau.
.
.png)
Khẳng định nào sau đây sai?
-
A.
Đường thẳng y = 2 cắt đồ thị hàm số tại 3 điểm phân biệt.
-
B.
Hàm số có điểm cực tiểu là x = - 2.
- C. \(f(x) = {x^3} + 3{x^2} - 4\).
- D. Hàm số nghịch biển trên khoảng (- 2;0).
-
A.
-
Câu 6: Mã câu hỏi: 127589
Cho \(a = 1 + {2^{ - x}}\), \(b = 1 + {2^x}\). Biểu thức biểu diễn b theo a là:
- A. \(\frac{{a + 2}}{{a - 1}}\).
- B. \(\frac{{a - 2}}{{a - 1}}\).
- C. \(\frac{{a - 1}}{a}\).
- D. \(\frac{a}{{a - 1}}\).
-
Câu 7: Mã câu hỏi: 127590
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình bên. Phát biểu nào sau đây là đúng?
- A. Hàm số đạt cực đại tại x = 1.
- B. Giá trị cực tiểu của hàm số là - 1.
- C. Hàm số đạt cực tiểu tại x = 1.
- D. Hàm số có 3 cực trị .
-
Câu 8: Mã câu hỏi: 127591
Cho hàm số \(y=f(x)\) có đạo hàm trên R và có đồ thị là đường cong như hình vẽ dưới đây.
.png)
Đặt \(g\left( x \right) = f\left( {f\left( x \right)} \right)\). Số nghiệm của phương trình \(g'\left( x \right) = 0\) là :
- A. 6
- B. 7
- C. 5
- D. 8
-
Câu 9: Mã câu hỏi: 127592
Đồ thị như hình vẽ là đồ thị của hàm số nào dưới đây?
- A. \(y = - {x^3} - {\rm{3}}{x^2} - 4.\)
- B. \(y = {x^3} - {\rm{3}}{x^2} + 4\).
- C. \(y = {x^3} - {\rm{3}}{x^2} - 4\).
- D. \(y = - {x^3}{\rm{ + 3}}{x^2} - 4\).
-
Câu 10: Mã câu hỏi: 127595
Để đường thẳng \(d:y = x - m + 2\) cắt đồ thị hàm số \(y = \frac{{2x}}{{x - 1}}\) (C) tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất thì giá trị của thuộc khoảng nào?
- A. \(m \in \left( { - 4; - 2} \right)\).
- B. \(m \in \left( {2;4} \right)\).
- C. \(m \in \left( { - 2;0} \right)\).
- D. \(m \in \left( {0;2} \right)\).
-
Câu 11: Mã câu hỏi: 127598
Cho hàm số \(y = \frac{{x + 1}}{{{x^2} - 2mx + 4}}\). Tìm tất cả các giá trị của tham số m để đồ thị có ba đường tiệm cận
- A. m > 2
-
B.
\(\left\{ \begin{array}{l}
m < - 2\\
m \ne - \frac{5}{2}
\end{array} \right.\) -
C.
\(\left[ \begin{array}{l}
m > 2\\
\left\{ \begin{array}{l}
m < - 2\\
m \ne - \frac{5}{2}
\end{array} \right.
\end{array} \right.\) -
D.
\(\left[ \begin{array}{l}
m > 2\\
m < - 2
\end{array} \right.\)
-
Câu 12: Mã câu hỏi: 127600
Một khối lập phương có cạnh bằng a (cm). Khi tăng kích thước của mỗi cạnh thêm 2cm thì thể tích của khối lăng trụ tăng thêm 98cm3. Giá trị a bằng:
- A. 4 cm
- B. 5 cm
- C. 3 cm
- D. 6 cm
-
Câu 13: Mã câu hỏi: 127603
Cho hàm số \(y = \frac{{1 - m\sin x}}{{\cos x + 2}}\). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;10] để giá trị nhỏ nhất của hàm số nhỏ hơn - 2?
- A. 6
- B. 9
- C. 3
- D. 1
-
Câu 14: Mã câu hỏi: 127607
Hàm số nào sau đây đạt cực tiểu tai điểm x = 0?
- A. \(y = {x^2} + 1\)
- B. \(y = {x^3} - 3{x^2} + 2\)
- C. \(y = - {x^3} + x - 1\)
- D. \(y = {x^3} + 2\)
-
Câu 15: Mã câu hỏi: 127610
Hàm số \(y = {\left( {x + m} \right)^3} + {\left( {x + n} \right)^3} - {x^3}\) đồng biến trên khoảng \(\left( { - \infty ;\, + \infty } \right)\). Giá trị nhỏ nhất của biểu thức \(P = 4\left( {{m^2} + {n^2}} \right) - m - n\) bằng
- A. \(\frac{{ - 1}}{{16}}\)
- B. - 16
- C. \(\frac{1}{4}\)
- D. 4
-
Câu 16: Mã câu hỏi: 127613
Một chất điểm chuyển động có phương trình \(S = 2{t^4} + 6{t^2} - 3t + 1\) với t tính bằng giây (s) và S tính bằng mét (m). Hỏi gia tốc của chuyển động tại thời điểm t = 3(s) bằng bao nhiêu?
- A. 76 (m/s2)
- B. 64 (m/s2)
- C. 228 (m/s2)
- D. 88 (m/s2)
-
Câu 17: Mã câu hỏi: 127616
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Cạnh bên SC vuông góc với mặt phẳng (ABC), SC = a. Thể tích khối chóp S.ABC bằng
- A. \(\frac{{{a^3}\sqrt 3 }}{3}\)
- B. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
- C. \(\frac{{{a^3}\sqrt 3 }}{9}\)
- D. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
-
Câu 18: Mã câu hỏi: 127619
Đường tiệm cận ngang của đồ thị hàm số \(y = {\mkern 1mu} \frac{{x - 3}}{{x - 1}}\) có phương trình là
- A. y = 1
- B. y = 5
- C. y = 0
- D. x = 1
-
Câu 19: Mã câu hỏi: 127622
Cho hàm số \(y = \frac{{8x - 5}}{{x + 3}}\). Kết luận nào sau đây đúng?
- A. Hàm số luôn đồng biến trên R.
- B. Hàm số luôn đồng biến trên từng khoảng xác định của nó.
- C. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 3} \right) \cup \left( { - 3; + \infty } \right)\).
- D. Hàm số nghịch biến trên khoảng (0;2).
-
Câu 20: Mã câu hỏi: 127623
Khối tứ diện đều có bao nhiêu cạnh?
- A. 6
- B. 4
- C. 5
- D. 9
-
Câu 21: Mã câu hỏi: 127624
Cho hàm số y = f(x) liên tục trên đoạn [- 1;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [- 1;3]. Giá trị của M - m bằng
.png)
- A. 4
- B. 5
- C. 0
- D. 1
-
Câu 22: Mã câu hỏi: 127625
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên:
.png)
Tìm m để phương trình \(2f\left( x \right) + m = 0\) có đúng 3 nghiệm phân biệt
- A. m = 4
- B. m = 2
- C. m = - 1
- D. m = - 2
-
Câu 23: Mã câu hỏi: 127626
Đồ thị đã cho là của hàm số nào?
.png)
- A. \(y = - {x^4} - 2{x^2} + 2\)
- B. \(y = - {x^4} + 2{x^2} + 2\)
- C. \(y = {x^4} - 2{x^2} + 2\)
- D. \(y = {x^4} + 2{x^2} - 2\)
-
Câu 24: Mã câu hỏi: 127627
Đồ thị hàm số \(y = \frac{{\sqrt {x - 3} }}{{{x^2} + x - 6}}\) có bao nhiêu đường tiệm cận?
- A. 0
- B. 2
- C. 3
- D. 1
-
Câu 25: Mã câu hỏi: 127628
Kết luận nào đúng về số thực a nếu \({(a - 1)^{ - \frac{2}{3}}} < {(a - 1)^{ - \frac{1}{3}}}\)
- A. a > 1
- B. a > 0
- C. a > 2
- D. 1 < a < 2
-
Câu 26: Mã câu hỏi: 127629
Số mặt phẳng đối xứng của hình chóp đều S.ABCD là
- A. 6
- B. 4
- C. 7
- D. 2
-
Câu 27: Mã câu hỏi: 127630
Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) trên khoảng (-1;2) như hình vẽ bên. Số điểm cực đại của hàm số y = f(x) trên khoảng (-1;2) là
.png)
- A. 2
- B. 1
- C. 0
- D. 3
-
Câu 28: Mã câu hỏi: 127632
Tiếp tuyến của đồ thị \(\left( C \right):y = \frac{{1 - x}}{{x + 1}}\) tại điểm có tung độ bằng 1 song song với đường thẳng
- A. \(\left( d \right):y = - 2x + 2\)
- B. \(\left( d \right):y = x - 1\)
- C. \(\left( d \right):y = -x + 1\)
- D. \(\left( d \right):y = 2x - 1\)
-
Câu 29: Mã câu hỏi: 127633
Cho hình chóp có 20 cạnh. Số mặt của hình chóp đó là
- A. 12
- B. 10
- C. 11
- D. 20
-
Câu 30: Mã câu hỏi: 127637
Cho hàm số y = f(x) có bảng biến thiên như sau:
.png)
Mệnh đề nào dưới đây đúng?
- A. Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)
- B. Hàm số nghịch biến trên \(\left( { - \infty ;0} \right) \cup \left( {1; + \infty } \right)\)
- C. Hàm số đồng biến trên (0;1)
- D. Hàm số đồng biến trên \(\left( { - \infty ;2} \right)\)
-
Câu 31: Mã câu hỏi: 127640
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) đạt cực tiểu tại điểm x = 1, \(f\left( 1 \right) = - 3\) và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính \(T=a+b+c\).
- A. T = 9
- B. T = 1
- C. T = - 2
- D. T = - 4
-
Câu 32: Mã câu hỏi: 127642
Giá trị cực đại của hàm số \( = - {x^3} + 3x\) là:
- A. - 1
- B. 1
- C. - 2
- D. 2
-
Câu 33: Mã câu hỏi: 127645
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{a\sqrt 3 }}{2}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
- A. 450
- B. 900
- C. 600
- D. 300
-
Câu 34: Mã câu hỏi: 127651
Hàm số \(y = {x^3} - 3{x^2} + 5\) đồng biến trên khoảng nào dưới đây?
- A. \(( - \infty ,0)\) và \((2; + \infty ).\)
- B. (0;2)
- C. \((0; + \infty ).\)
- D. \(( - \infty ,2)\)
-
Câu 35: Mã câu hỏi: 127654
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây.
.png)
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) - 1}}\) là
- A. 0
- B. 2
- C. 3
- D. 1
-
Câu 36: Mã câu hỏi: 127657
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = - {x^4} + 8{x^2} - 2\) trên đoạn [-3;1]. Tính M + m?
- A. - 25
- B. - 48
- C. 3
- D. - 6
-
Câu 37: Mã câu hỏi: 127660
Cho các số thực \(a,b,\alpha \left( {a > b > 0,\alpha \ne 1} \right)\). Mệnh đề nào sau đây đúng?
- A. \({\left( {a + b} \right)^\alpha } = {a^\alpha } + {b^\alpha }.\)
- B. \({\left( {a - b} \right)^\alpha } = {a^\alpha } - {b^\alpha }\)
- C. \({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }.\)
- D. \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^{ - \alpha }}}}.\)
-
Câu 38: Mã câu hỏi: 127661
Khối lập phương thuộc loại khối đa diện đều nào?
- A. {3;3}
- B. {3;4}
- C. {4;3}
- D. {5;3}
-
Câu 39: Mã câu hỏi: 127663
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?
- A. \(S = \sqrt 3 {a^2}\)
- B. \(S = 8{a^2}\)
- C. \(S = 2\sqrt 3 {a^2}\)
- D. \(S =4 \sqrt 3 {a^2}\)
-
Câu 40: Mã câu hỏi: 127666
Trong các hình dưới đây hình nào không phải đa diện lồi?
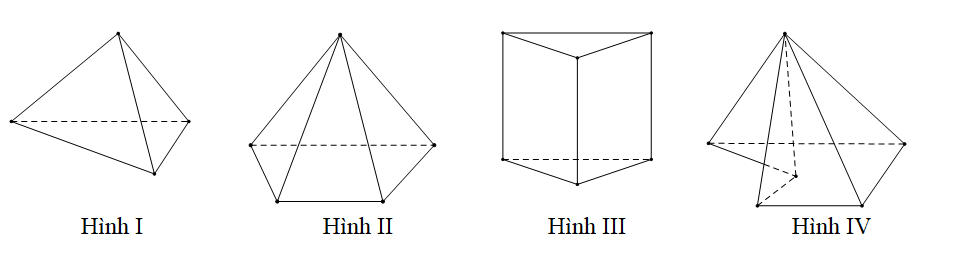
- A. Hình (III).
- B. Hình (I).
- C. Hình (II).
- D. Hình (IV).
-
Câu 41: Mã câu hỏi: 127671
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại B, đường cao BH. Biết \(A'H \bot \left( {ABC} \right)\) và \(AB = 1,AC = 2,AA' = \sqrt 2 \). Thể tích của khối lăng trụ đã cho bằng
- A. \(\frac{{\sqrt {21} }}{{12}}\)
- B. \(\frac{{\sqrt 7 }}{4}\)
- C. \(\frac{{\sqrt {21} }}{4}\)
- D. \(\frac{{3\sqrt 7 }}{4}\)
-
Câu 42: Mã câu hỏi: 127675
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^4} + \left( {m - 1} \right){x^2} + {m^2}\) đạt cực tiểu tại x = 0
- A. \(m \ge 1\)
- B. \(m \le 1\)
- C. \(m\in R\)
- D. m = 1
-
Câu 43: Mã câu hỏi: 127678
Cho số thực dương a. Biểu thức \(P = \sqrt {a\sqrt[3]{{a\sqrt[4]{{a\sqrt[5]{a}}}}}} \) được viết dưới dạng lũy thừa với số mũ hữu tỉ là
- A. \({a^{\frac{{53}}{{36}}}}\)
- B. \({a^{\frac{{25}}{{13}}}}\)
- C. \({a^{\frac{{37}}{{13}}}}\)
- D. \({a^{\frac{{43}}{{60}}}}\)
-
Câu 44: Mã câu hỏi: 127681
Mệnh đề nào sau đây là sai?
- A. Tứ diện là một hình đa diện.
- B. Mỗi cạnh của hình đa diện là cạnh chung của ít nhất ba mặt.
- C. Hình chóp có số cạnh bên bằng số cạnh đáy.
- D. Hình lăng trụ có tất cả các mặt bên là hình thang.
-
Câu 45: Mã câu hỏi: 127685
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}\), có đồ thị như hình vẽ. Tính \(T=a+b\)
.png)
- A. T = 3
- B. T = 2
- C. T = 0
- D. T = - 1
-
Câu 46: Mã câu hỏi: 127689
Cho hình chóp tam giác S.ABC có \(SA = x,BC = y\), các cạnh còn lại bằng 1. Tính thể tích khối chóp S.ABC theo x, y.
- A. \(V = \frac{{xy}}{{12}}\sqrt {4 + {x^2} + {y^2}} \)
- B. \(V = \frac{{xy}}{{12}}\sqrt {4 - {x^2} - {y^2}} \)
- C. \(V = \frac{{xy}}{{24}}\sqrt {4 - {x^2} - {y^2}} \)
- D. \(V = \frac{{xy}}{{24}}\sqrt {4 + {x^2} + {y^2}} \)
-
Câu 47: Mã câu hỏi: 127696
Cho hình chóp S.ABC có thể tích bằng V. Gọi G là trọng tâm tam giác SBC. Mặt phẳng \((\alpha )\) đi qua hai điểm A, G và song song với BC. Mặt phẳng \((\alpha )\) cắt các cạnh SB, SC lần lượt tại các điểm M và N. Thể tích khối chóp S.AMN bằng
- A. \(\frac{V}{9}\)
- B. \(\frac{V}{2}\)
- C. \(\frac{{4V}}{9}\)
- D. \(\frac{V}{4}\)
-
Câu 48: Mã câu hỏi: 127702
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(\sqrt 2 a\). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\frac{4}{3}{a^3}\). Tính khoảng cách h từ B đến mặt phẳng (SCD).
- A. \(h = \frac{4}{3}a\)
- B. \(h = \frac{3}{2}a\)
- C. \(h = \frac{{2\sqrt 5 }}{5}a\)
- D. \(h = \frac{{\sqrt 6 }}{3}a\)
-
Câu 49: Mã câu hỏi: 127706
Cho hình chóp S.ABCD có đáy ABCD là hình vuông đường chéo \(AC = 2\sqrt 2 \,a\). Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với (ABCD). Thể tích của khối chóp S.ABCD là:
- A. \(a^3\)
- B. \(\frac{{4\sqrt 3 \,{a^3}}}{3}\)
- C. \(\frac{{\sqrt 3 \,{a^3}}}{6}\)
- D. \(\frac{{2\sqrt 3 \,{a^3}}}{3}\)
-
Câu 50: Mã câu hỏi: 127707
Giá trị lớn nhất của hàm số \(\left( x \right) = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn [-1;2] là:
- A. 15
- B. 10
- C. 6
- D. 11





.PNG)
.PNG)

