Câu 1: Con lắc đơn (vật nặng khối lượng m, dây treo dài 1 m) dao động điều hòa dưới tác dụng của ngoại lực \(F = F_0\cos(2 \pi ft + \frac{\pi}{2})\). Lấy \(g = \pi ^2 = 10\ m/s^2\). Nếu tần số f của ngoại lực thay đổi từ 1 Hz đến 2 Hz thì biên độ dao động của con lắc
A. không thay đổi.
B. tăng rồi giảm.
C. luôn tăng.
D. luôn giảm.

Lời giải:
CLĐ: \(\ell = 1\ m;\ g = \pi ^2 = 10 \ \frac{m}{s^2}\)
\(F = F_0\cos (2 \pi f t + \frac{\pi }{2})\)
Thay đổi f từ 1 Hz đến 2 Hz
+ Tần số riêng: \(f_0 = \frac{1}{2\pi }\sqrt{\frac{g}{\ell}} = \frac{1}{2}\ Hz\)
+ Ta có:
\(|f_1 - f_0| = \left | 1 - \frac{1}{2} \right | = \frac{1}{2}\)
\(|f_2 - f_0| = \left | 2 - \frac{1}{2} \right | = \frac{3}{2}\)
\(\Rightarrow |f_1 - f_0| < |f_1 - f_0|\)
⇒ A₁ > A₂ ⇒ luôn giảm
⇒ Chọn D

Câu 2: Một chiếc xe máy chạy trên một con đường lát gạch, cứ cách khoảng 4 m trên đường lại có một cái rãnh nhỏ. Chu kì dao động riêng của khung xe máy trên các lò xo giảm xóc là 0,5 s. Xe bị xóc mạnh nhất khi vận tốc bằng
A. 28,8 km/h.
B. 7,2  km/h.
C. 48  km/h.
D. 24,6 km/h.

Lời giải:
S = 4 m
T₀ = 0,5 s
Xe bị húc mạnh nhất ⇒ Xảy ra cộng hưởng
\(\Rightarrow T = T_0 \Rightarrow v = \frac{S}{T} = \frac{S}{T_0}\)
\(\Rightarrow v = \frac{4}{0,5} = 8\ \frac{m}{s} = 8 \times 3,6 = 25,8\ \frac{km}{h}\)
⇒ Chọn A

Câu 3: Một con lắc lò xo gồm vật nhỏ khối lượng 0,02 kg và lò xo có độ cứng 1 N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,1. Ban đầu giữ vật ở vị trí lò xo bị nén 10 cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10 m/s². Tốc độ lớn nhất vật nhỏ đạt được trong quá trình dao động là
A. 40 cm/s.
B. 20 cm/s.
C. 10 cm/s.
D. 40 cm/s.

Lời giải:
\(m = 0,02\ kg;\ k = 1\ \frac{N}{m};\ \mu =0,1;\ A = 10\ cm\)
\(+\ v_{max} = (A - x_0)\omega\)
\(+\ x_0 = \frac{\mu mg}{k} = \frac{0,1.0,02.10 }{1} = 0,02\ m = 2\ cm\)
\(\Rightarrow v_{max} = (10 - 2).\sqrt{\frac{1}{0,02}} = 40\sqrt{2}\ \frac{cm}{s}\)
⇒ Chọn D

Câu 4: Một vật dao động riêng với tần số là f = 10Hz. Nếu tác dụng vào vật ngoại lực có tần số f₁ = 12Hz thì biên độ là A₁. Nếu tác dụng vào vật ngoại lực có tần số biến đổi là f₂ = 14 Hz và cùng giá trị biên độ với ngoại lực thứ nhất thì vật dao động với biên độ A₂ (mọi điều kiện khác không đổi). Tìm phát biểu đúng?
A. A₁ > A₂.
B. A₁ < A₂.
C. A₁ = A₂.
D. Không kết luận được.

Lời giải:
f₀ = 10 Hz; f₁ = 12 Hz; f₂ = 14Hz
Biên độ của ngoại lực không đổi
Ta có: \(\left.\begin{matrix} |f_1 - f_0| = 2\\ |f_2 - f_0| = 4 \end{matrix}\right\} \Rightarrow |f_1 - f_0| < |f_2 - f_0| \Rightarrow A_1 > A_2\)
⇒ Chọn A

Câu 5: Một con lắc lò xo độ cứng k = 400 N/m; m = 0,1kg được kích thích bởi 2 ngoại lực sau
- Ngoại lực 1 có phương trình \(f = F\cos(8 \pi t + \frac{\pi }{3})\) (N) thì biên độ dao động là A₁.
- Ngoại lực 2 có phương trình \(f = F\cos(6 \pi t + \frac{\pi }{2})\) (N) thì biên độ dao động là A₂.
Tìm nhận xét đúng.
A. A₁ = A₂.
B. A₁ > A₂.
C. A₁ < A₂.
D. A và B đều đúng.

Lời giải:
\(k = 400\ \frac{N}{m};\ m = 0,1\ kg \Rightarrow \omega _0 = \sqrt{\frac{k}{m}} = 20\pi \ \frac{rad}{s}\)
\(f_1 = F_0.\cos (8 \pi t + \frac{\pi }{3})\ (N) \rightarrow A_1\)
\(f_2 = F_0.\cos (6 \pi t + \frac{\pi }{2})\ (N) \rightarrow A_2\)
Ta có: \(\left.\begin{matrix} |\omega _1 - \omega _0| = 12 \pi \\ |\omega _2 - \omega _0| = 14 \pi \end{matrix}\right\} \Rightarrow |\omega _1 - \omega _0| < |\omega _2 - \omega _0| \Rightarrow A_1 > A_2\)
⇒ Chọn B

Câu 6: Một con lắc lò xo nếu chịu tác dụng của hai ngoại lực f₁ = 8 Hz và f₂ = 10 Hz có cùng độ lớn biên độ thì thấy biên độ dao động cưỡng bức là như nhau A₁ = A₂. Dùng ngoại lực f₃ = 9 Hz và có biên độ như ngoại lực thứ nhất và thứ hai thì biên độ dao động cưỡng bức sẽ là A₃. Dùng ngoại lực f₄ = 12 Hz và có biên độ như ngoại lực thứ nhất và thứ hai thì biên độ dao động cưỡng bức sẽ là A₄. Tìm nhận xét đúng
A. A₃ > A₁ = A₂ > A₄.
B. A₃ < A₁ = A₂ = A₄.
C. A₃ = A₁ = A₂ < A₄.
D. A₃ < A₁ = A₂ < A₄.

Lời giải:
\(\\ f_1 = 8\ Hz \rightarrow A_1 \\ f_2 = 10\ Hz \rightarrow A_2 = A_1 \\ f_3 = 9\ Hz \rightarrow A_3 \\ f_4 = 12\ Hz \rightarrow A_4\)
Biên độ của ngoại lực không đổi
\(+\ A_2 = A_1 \Rightarrow |f_2 - f_0| = |f_1 - f_0|\)
\(\Rightarrow \bigg \lbrack \begin{matrix} f_2 - f_0 = f_1 - f_0 \ (loai) \hspace{3cm}\\ f_2 - f_0 = -f_1 + f_0 \Rightarrow f_0 = \frac{f_1 + f_2}{2} = 9\ Hz \end{matrix}\)
\(f =f_0 = 9\ Hz \Rightarrow A_{max} = A_3 \Rightarrow A_3 > A_1 = A_2\)
\(+\ |f_1 - f_0| < |f_4 - f_0| \Rightarrow A_1 > A_4\)
\(\Rightarrow A_3 > A_1 = A_2 > A_4\)
⇒ Chọn A

Câu 7: Một con lắc lò xo có độ cứng k = 100N/m và vật nặng m = 0,1 kg. Hãy tìm nhận xét đúng
A. Khi f_nl < 10 Hz thì khi tăng tần số thì biên độ dao động cưỡng bức luôn tăng.
B. Khi f_nl < 5 Hz thì khi tăng tần số thì biên độ dao động cưỡng bức giảm rồi tăng.
C. Khi f_nl > 5 Hz thì khi tăng tần số thì biên độ dao động cưỡng bức tăng rồi giảm.
D. Khi f_nl > 10 Hz thì khi tăng tần số thì biên độ dao động cưỡng bức luôn giảm.

Lời giải:
\(k = 100\ \frac{N}{m}; \ m = 0,1\ kg\)
\(\Rightarrow f_0 = \frac{1}{2\pi }\sqrt{\frac{k}{m}} = 5\ Hz\)

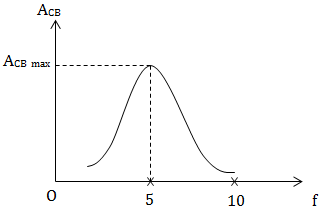
f_nℓ > 10 Hz
 Và tăng f_nℓ ⇒ (ACB) luôn giảm
⇒ Chọn D

Câu 8: Một con lắc lò xo có  độ cứng và khối lượng lần lượt như sau: k = 100 N/m; m = 0,1 kg; Nếu chịu tác dụng của ngoại lực có tần số  f_nl = 2 Hz. Hỏi khi ổn định con lắc lò xo trên dao động với tần số bằng bao nhiêu?
A. 3 Hz.
B. 5 Hz.
C. 7 Hz.
D. 2 Hz

Lời giải:
CLLX: \(k = 100\ \frac{N}{m}; m = 0,1\ kg\)
f_nℓ = 2 Hz ⇒ f_dđ = f_nℓ = 2 Hz
⇒ Chọn D

Câu 9: Một con lắc lò xo có độ cứng k = 100 N/m và khối lượng m, chịu tác dụng của ngoại lực có phương trình \(F= 0,1\cos(10 t + \frac{\pi }{2})\) N thì biên độ dao động của vật đạt cực đại. Giá trị của m bằng
A. 100 g.
B. 1 kg.
C. 500 g.
D. 50 g.

Lời giải:
\(k = 100\ \frac{N}{m};\ F = 0,1.\cos (10t + \frac{\pi }{2}) \ (N)\)
(A_CB)_max ⇒ Xảy ra cộng hưởng
\(\Rightarrow \omega _0 = \omega _{n\ell } \Rightarrow \sqrt{\frac{k}{m}} = 10 \Rightarrow m = \frac{k}{10^2} = 1\ kg\)
⇒ Chọn B

Câu 10: Con lắc lò xo có độ cứng k, khối lượng vật nặng  m = 1 kg. Vật nặng đang đứng ở vị trí cân bằng, ta tác dụng lên con lắc một ngoại lực biến đổi điều hòa theo thời gian với phương trình F = F₀cos10t N. Sau một thời gian ta thấy vật dao động ổn định với tốc độ dao động cực đại là v_max = 50 cm/s. Xác  định biên độ của dao động
A. 5 cm.
B. 0,5 cm.
C. 0,25 cm.
A. 2,5 cm.

Lời giải:
\(m = 1\ kg;\ F = F_0\cos 10t \ (N);\ v_{max} = 50\ \frac{cm}{s}\)
\(\omega\)_{dao động} \(= \omega _{n\ell} = 10\ \frac{rad}{s}\)

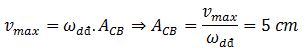
⇒ Chọn A

Câu 11: Một con lắc lò xo có độ cứng k và vật nặng khối lượng là m. Nếu dùng ngoại lực thứ nhất \(F_1 = 0,5\cos(\omega t + \varphi )\) N kích thích thì khi ổn định biên độ dao động cưỡng bức là A₁. Nếu dùng ngoại lực thứ hai \(F_2 = \cos(\omega t + \varphi )\) N kích thích thì khi ổn định biên độdao động cưỡng bức là A₂ . Coi lực cản môi trường là như nhau. Hãy tìm phát biểu đúng?
A. A₁ > A₂.
B. A₁ < A₂.
C. A₁ = A₂.
D. Không thể kết luận.

Lời giải:
\(\\ F_1 = 0,5\cos (\omega t + \varphi ) \rightarrow A_1 \\ F_2 = \cos (\omega t + \varphi ) \rightarrow A_2\)
Lực cản như nhau
Ta có: \(\left.\begin{matrix} F_{01} = 0,5\ N\\ F_{02} = 1\ N \ \ \ \end{matrix}\right\} \Rightarrow F_{02} > F_{01} \Rightarrow A_2 > A_1\)
⇒ Chọn B

Câu 12: Một con lắc đơn có ℓ = 1m; g = 10m/s² được treo trên một xe ôtô, khi xe đi qua phần đường mấp mô, cứ 12m lại có một chỗ ghềnh, tính vận tốc của vật để con lắc dao động mạnh nhất.
A. 6m/s.
B. 6km/h.
C. 60km/h.
D. 36km/s.

Lời giải:
CLĐ: \(\ell = 1\ m;\ g = 10\ \frac{m}{s^2};\ S = 12\ m\)
Con lắc dao động mạnh nhất ⇒ A_max ⇒ Xảy ra cộng hưởng
\(\Rightarrow T = T_0 = 2\pi \sqrt{\frac{\ell}{g}} = 2s\)
\(\Rightarrow v = \frac{S}{T} = \frac{12}{2} = 6\ \frac{m}{s}\)
⇒ Chọn A

Câu 13: Một tấm ván có tần số riêng là 2Hz. Hỏi trong một 1 phút một người đi qua tấm ván phải đi bao nhiêu bước để tấm ván rung mạnh nhất:
A. 60 bước.
B. 30 bước.
C. 60 bước.
D. 120 bước.

Lời giải:
+ f₀ = 2 Hz;
+ ∆t = 1 phút = 60 s
+ Bao nhiêu bước ⇒ Tấm ván rung mạnh nhất
\(\Rightarrow f = f_0 = \frac{n}{\Delta t} \Rightarrow n = f_0.\Delta t = 120\) bước
⇒ Chọn D

Câu 14: Một vật dao động tắt dần cứ sau mỗi chu kỳ biên độ giảm 3%, tính phần năng lượng còn lại trong một chu kỳ?
A. 94%.
B. 96%.
C. 95%.
D. 91%.

Lời giải:
\(\left\{\begin{matrix} E = \frac{1}{2}m\omega ^2A^2 \hspace{3,4cm}\\ E' = \frac{1}{2}m\omega ^2A'^{2} = \frac{1}{2}m\omega ^2.(0,97A^2) \end{matrix}\right.\)
\(\frac{E'}{E} = 0,97^2 = 94\%\)
⇒ Chọn A

Câu 15: Một con lắc lò xo độ cứng 100 N/m dao động tắt dần trên mặt phẳng ngang. Ban đầu kéo vật lệch khỏi vị trí cân bằng một đoạn 5 cm rồi buông tay không vận tốc đầu. Hệ số ma sát của vật và mặt phẳng ngang là µ = 0,01. Vật nặng 100g, g = \(\pi\)² = 10m/s². Hãy xác định vị trí tại đó vật có tốc độ cực đại
A. 0,01 m.
B. 0,001 m.
C. 0,001 m.
D. 0,0001 m.

Lời giải:
\(k = 100\ \frac{N}{m}; A = 5\ cm; \mu = 0,01\)
\(m = 100\ g = 0,1 \ kg; g = 10\ \frac{m}{s^2}\)
\(+ \ v_{max} \Rightarrow x_0 = \frac{\mu mg}{k} = \frac{0,01.0,1.10}{100} = 0,0001\ m\)
⇒ Chọn D

Câu 16: Một con lắc lò xo độ cứng k = 100 N/m dao động tắt dần trên mặt phẳng ngang. Ban đầu kéo vật lệch khỏi vị trí cân bằng cho lò xo dãn một đoạn 5 cm rồi buông tay không vận tốc đầu. Hệ số ma sát của vật và mặt phẳng ngang là μ = 0,01. Biết vật nặng m = 100 g, g = \(\pi\)² = m/s². Hãy xác định độ nén lớn nhất của lò xo trong quá trình dao động?
A. 4,98 cm.
B. 4,88 cm.
C. 4,96 cm.
D. 5 cm.

Lời giải:
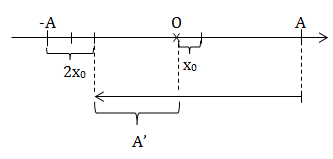
\(k = 100\ \frac{N}{m}\); lò xo dãn 5 cm ⇒ A = 5 cm
\(\mu = 0,1;\ m = 0,1 \ kg;\ g = \pi ^2 = 10\ \frac{m}{s^2}\)
\(+\ x_0 = \frac{\mu mg}{k} = \frac{0,01.0,1.10}{100} = 0,0001\ m = 0,01\ cm\)
+ Độ giảm biên độ sau nửa chu kỳ:
\(\Delta A' = 2x_0 = 2.0,01\ cm = 0,02\ cm\)
+ (X_nén)_max = A' = A - ∆A = 4,98 cm
⇒ Chọn A

Câu 17: Con lắc đơn gồm sợi dây nhẹ không giãn có độ dài ℓ = 1 m, một đầu cố định, một đầu gắn với hòn bi khối lượng m. Kéo vật ra khỏi vị trí cân bằng sao cho sợi dây hợp với phương thẳng đứng góc 0,1 rad rồi thả nhẹ. Trong quá trình dao động con lắc luôn chịu tác dụng của lực cản có độ lớn bằng \(F_C = \frac{P}{1000}\) (trong đó P là trọng lực tác dụng lên vật). Coi chu kỳ dao động là không đổi trong quá trình dao động và biên độ dao động giảm đều trong từng nửa chu kỳ. Xác định thời gian con lắc dao động kể từ ban đầu đến khi dừng hẳn. Lấy g = \(\pi\)² = 10m/s².
A. 55 s.
B. 150 s.
C. 50 s.
D. 250 s.

Lời giải:
\(\ell = 1\ m;\ \alpha _0 = 0,1\ rad\)
\(F_C = \frac{P}{1000} = \frac{mg}{1000}\)
\(+\ \Delta t = N.T = \frac{A}{\Delta A}.T = \frac{S_0}{\Delta s}.T\)
    \(\\ \cdot \ T = 2\pi \sqrt{\frac{\ell}{g}} = 2\ s \\ \cdot \ S_0 = \alpha _0.\ell = 0,1.1 = 0,1 \ (m) \\ \cdot \ \Delta s = 4.\frac{F_C}{m\omega ^2} = 4.\frac{mg}{1000.m.\frac{g}{\ell}} = 0,004\ m\)
\(\Rightarrow \Delta t = \frac{0,1}{0,004} \times 2 = 50\ s\)
⇒ Chọn C

Câu 18: Một con lắc lò xo độ cứng k = 10 N/m, vật nặng có khối lượng m = 0,1 kg được đặt trên mặt phẳng ngang có hệ số ma sát trượt giữa vật và mặt sàn là 0,1. Ban đầu kéo vật lệch khỏi vị trí cân bằng một đoạn 10 cm rồi buông tay không vận tốc đầu cho vật dao động tắt dần. Chọn gốc tọa độ tại vị trí cân bằng, chiều dương theo chiều kéo vật, gốc thời gian lúc buông tay. Lấy g = \(\pi\)² = 10m/s². Quãng đường vật đi được trong chu kỳ thứ hai?
A. 16 cm.
B. 24 cm.
C. 10 cm.
D. 32 cm.

Lời giải:
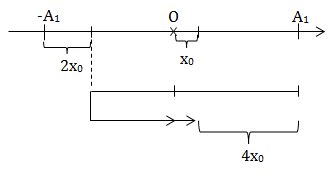
\(k = 10\ \frac{N}{m};\ m = 0,1\ kg;\ \mu = 0,1;\ A = 10\ cm\)
\(+\ x_0 = \frac{\mu mg}{k} = \frac{0,1.0,1.10}{10} = 0,01\ m = 1\ cm\)
+ Biên độ của vật sau chu kì đầu tiên:
A₁ = A - 4x₀ = 10 - 4.1 = 6 cm
+ Quãng đường vật đi được trong chu kì thứ 2:
S = 4A₁ - 8x₀ = 24 - 8 = 16 cm
⇒ Chọn A

Câu 19: Một con lắc lò xo độ cứng k = 10 N/m, vật nặng có khối lượng m = 0,1 kg được đặt trên mặt phẳng ngang có hệ số ma sát trượt giữa vật và mặt sàn là µ_t = 0,1. Ban đầu kéo vật lệch khỏi vị trí cân bằng một đoạn 12 cm rồi buông tay không vận tốc đầu cho vật dao động tắt dần. Lấy g = \(\pi\)² = 10m/s². Số dao động vật thực hiện được kể từ lúc đầu đến lúc tắt hẳn?
A. 1.
B. 2.
C. 4.
D. 3.

Lời giải:
\(k = 10\ \frac{N}{m};\ m = 0,1\ kg; \mu = 0,1;\ A = 12\ cm\)
\(+\ x_0 = \frac{\mu mg}{k} = \frac{0,1.0,1.10}{10} = 0,01 \ m = 1 \ cm\)
\(+\ \Delta A = 4x_0 = 4\ cm\)
+ Số dao động vật thực hiện từ lúc bắt đầu dao động đến khi tắt hẳn:
\(N = \frac{A}{\Delta A} = \frac{12}{4} = 3\)
⇒ Chọn D

Câu 20: Một con lắc lò xo có độ cứng là k = 100 N/m. Con lắc dao động với biên độ ban đầu là A₀ = 5 cm. Giả sử biên độ giảm đều sau mỗi chu kỳ và sau mỗi chu kỳ biên độ giảm 1% so với ban đầu. Sau bao nhiêu chu kỳ kể từ ban đầu để biên độ chỉ còn A₁ = 4 cm?
A. 100.
B. 10.
C. 20.
D. 36.

Lời giải:
\(k = 100\ \frac{N}{m};\ A_0 = 5\ cm\)

+ Theo đề bài: \(A_0 - n.\Delta A = A_1\)
\(\Rightarrow 5 - n. \frac{1}{100}.5 = 4\)
\(\Rightarrow \frac{n}{20} = 1 \Rightarrow n = 20\) dao động
⇒ Chọn C