Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 466301
Trên khoảng \(\left( 0;+\infty \right)\), đạo hàm của hàm số sau \(y={{\log }_{2}}x\) là?
- A. \(y'=\frac{1}{x\ln 2}\).
- B. \(y'=\frac{\ln 2}{x}\).
- C. \(y'=\frac{1}{x}\).
- D. \(y'=\frac{1}{2x}\).
-
Câu 2: Mã câu hỏi: 466305
Tập nghiệm của bất phương trình sau \({{2}^{x+1}}>8\) là?
- A. \(\left( -\infty ;2 \right)\).
- B. \(\left( -\infty ;2 \right]\).
- C. \(\left[ 2;+\infty \right)\).
- D. \(\left( 2;+\infty \right)\).
-
Câu 3: Mã câu hỏi: 466307
Cho số phức sau \(z=-4+5i\). Biểu diễn hình học của \(z\) là điểm có tọa độ?
- A. \(\left( -4;-5 \right)\)
- B. \(\left( -4;5 \right)\)
- C. \(\left( 4;-5 \right)\)
- D. \(\left( 4;5 \right)\)
-
Câu 4: Mã câu hỏi: 466312
Trên khoảng \(\left( 0;+\infty \right)\), đạo hàm của hàm số \(y={{x}^{e}}\) là?
- A. \({y}'=e{{x}^{e+1}}\).
- B. \({y}'=e{{x}^{e-1}}\).
- C. \({y}'=\frac{1}{e}{{x}^{e-1}}\).
- D. \({y}'=\frac{1}{e+1}{{x}^{e+1}}\).
-
Câu 5: Mã câu hỏi: 466317
Cho CSC \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=3\) và \({{u}_{2}}=-1\). Công sai của cấp số cộng đó bằng?
- A. 1
- B. -4
- C. 4
- D. 2
-
Câu 6: Mã câu hỏi: 466322
Cho biết \(\int\limits_{1}^{2}{f\left( x \right)\text{d}x=6}\), \(\int\limits_{2}^{5}{f\left( x \right)\text{d}x=1}\), tính \(I=\int\limits_{1}^{5}{f\left( x \right)\text{d}x}\)?
- A. \(I=5\).
- B. \(I=-5\).
- C. \(I=7\).
- D. \(I=4\).
-
Câu 7: Mã câu hỏi: 466323
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2y+4z-2=0\). Tính bán kính mặt cầu bằng?
- A. \(1\).
- B. \(\sqrt{7}\).
- C. \(2\sqrt{2}\).
- D. \(7\).
-
Câu 8: Mã câu hỏi: 466325
Đồ thị hàm số nào có dạng như đường cong trong hình bên?
.png)
- A. \(y=-{{x}^{4}}+2{{x}^{2}}\).
- B. \(y=-{{x}^{3}}+3x\).
- C. \(y={{x}^{4}}-2{{x}^{2}}\).
- D. \(y=-{{x}^{4}}-3{{x}^{2}}\).
-
Câu 9: Mã câu hỏi: 466326
Cho hàm số \(y=\frac{ax+b}{cx+d}\) có đồ thị là đường cong trong hình. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là?
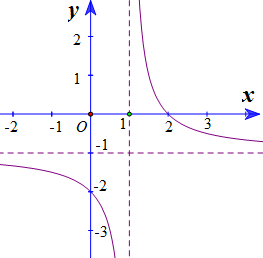
- A. \(\left( 0\,;\,2 \right)\).
- B. \(\left( 2\,;\,0 \right)\).
- C. \(\left( 0\,;\,-2 \right)\).
- D. \(\left( 1\,;\,0 \right)\).
-
Câu 10: Mã câu hỏi: 466327
Trong không gian \(Oxyz\), cho 3 điểm \(M\left( 2;1;-3 \right)\), \(N\left( 1;0;2 \right)\); \(P\left( 2;-3;5 \right)\). Tìm 1 vectơ pháp tuyến \(\overrightarrow{n}\) của mặt phẳng \(\left( MNP \right)\)?
- A. \(\overrightarrow{n}\left( 12;4;8 \right)\).
- B. \(\overrightarrow{n}\left( 8;12;4 \right)\).
- C. \(\overrightarrow{n}\left( 3;1;2 \right)\).
- D. \(\overrightarrow{n}\left( 3;2;1 \right)\).
-
Câu 11: Mã câu hỏi: 466329
Trong không gian \(Oxy\), góc giữa 2 trục \(Ox\) và \(Oz\) bằng?
- A. \({{30}^{\circ }}\)
- B. \({{45}^{\circ }}\)
- C. \({{60}^{\circ }}\)
- D. \({{90}^{\circ }}\)
-
Câu 12: Mã câu hỏi: 466333
Cho khối lăng trụ đứng có chiều cao bằng \(3\) và đáy là tam giác đều có độ dài cạnh bằng 2. Tính thể tích của khối lăng trụ đã cho?
- A. \(3\).
- B. \(3\sqrt{3}\).
- C. \(\sqrt{3}\).
- D. \(6\).
-
Câu 13: Mã câu hỏi: 466336
Trong không gian \(Oxyz\), cho hai mặt cầu \(\left( S \right):\,\,{{\left( x-3 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=9\) và \(\left( S' \right):\,\,{{\left( x+2 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=4\). Khẳng định nào đúng?
- A. Hai mặt cầu tiếp xúc ngoài.
- B. Hai mặt cầu tiếp xúc trong.
- C. Hai mặt cầu không có điểm chung.
- D. Hai mặt cầu có nhiều hơn một điểm chung.
-
Câu 14: Mã câu hỏi: 466337
Diện tích xung quanh Sxq của hình nón có bán kính đáy \(r=5cm\) và độ dài đường sinh \(l=7cm\) bằng?
- A. \(60\pi \,(c{{m}^{2}})\)
- B. \(175\pi \,(c{{m}^{2}}).\)
- C. \(70\pi \,(c{{m}^{2}}).\)
- D. \(35\pi \,(c{{m}^{2}}).\)
-
Câu 15: Mã câu hỏi: 466339
Cho hàm số \(y=a x^4+b x^2+c\) có đồ thị là đường cong trong hình bên. Điểm CT của đồ thị hàm số đã cho có tọa độ là?
- A. \((-1;1)\).
- B. \((0; 1)\).
- C. \((1;1)\).
- D. \((0;0)\).
-
Câu 16: Mã câu hỏi: 466343
TCĐ của đồ thị hàm số \(y=\frac{x-1}{x-3}\) là đường thẳng có phương trình?
- A. \(x=-3\).
- B. \(x=-3\).
- C. \(x=1\).
- D. \(x=1\).
-
Câu 17: Mã câu hỏi: 466345
Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right)\) có phương trình \(x+2y-3z-2=0\). Điểm nào thuộc mặt phẳng \(\left( P \right)\)?
- A. \(\left( 1;2;-3 \right)\).
- B. \(\left( -1;2;3 \right)\).
- C. \(\left( 1;2;1 \right)\).
- D. \(\left( 1;2;-2 \right)\).
-
Câu 18: Mã câu hỏi: 466347
Phần thực của số phức sau đây \(z=4-2i\) bằng?
- A. \(-2\).
- B. \(-4\).
- C. 2
- D. 4
-
Câu 19: Mã câu hỏi: 466349
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông tại \(B.\) Biết \(BC=a\sqrt{3}\,,\ AB=a\), \(SA\) vuông góc với đáy, \(SA=2a\sqrt{3}\). Tính thể tích khối chóp \(S.ABC\) bằng?
.png)
- A. \({{a}^{3}}\sqrt{3}.\)
- B. \(\frac{{{a}^{3}}\sqrt{3}}{3}.\)
- C. \(3{{a}^{3}}.\)
- D. \({{a}^{3}}.\)
-
Câu 20: Mã câu hỏi: 466351
Cho số phức sau \(z=3+5i\), phần ảo của số phức \({{\bar{z}}^{2}}\) bằng?
- A. \(16\).
- B. \(30\).
- C. \(-16\).
- D. \(-30\).
-
Câu 21: Mã câu hỏi: 466353
Tập nghiệm của bất phương trình sau \(lo{{g}_{2}}\left( x+1 \right)<3\) là?
- A. \(S=\left( -\infty ;\,\,8 \right)\).
- B. \(S=\left( -\infty ;\,\,7 \right)\).
- C. \(S=\left( -1;\,\,8 \right)\).
- D. \(S=\left( -1;\,\,7 \right)\).
-
Câu 22: Mã câu hỏi: 466355
Cho \(\int{\cos 3x.dx}=F\left( x \right)+C\). Khẳng định nào đúng?
- A. \({F}'\left( x \right)=\frac{\sin 3x}{3}\).
- B. \({F}'\left( x \right)=\cos 3x\).
- C. \({F}'\left( x \right)=3\sin 3x\).
- D. \({F}'\left( x \right)=-3\sin 3x\).
-
Câu 23: Mã câu hỏi: 466360
Họ tất cả các nguyên hàm của hàm số sau \(f\left( x \right)=3{{x}^{2}}-2\cos x\) là?
- A. \(F\left( x \right)=3{{x}^{3}}+2\sin x+C\).
- B. \(F\left( x \right)={{x}^{3}}-2\sin x+C\).
- C. \(F\left( x \right)=3{{x}^{3}}-2\sin x+C\).
- D. \(F\left( x \right)={{x}^{3}}+\sin x+C\).
-
Câu 24: Mã câu hỏi: 466363
Cho \(\int\limits_{2}^{4}{f\left( x \right)\text{d}x}=10\). Tính giá trị của \(I=\int\limits_{2}^{4}{\left[ 3f\left( x \right)-5 \right]\text{d}x}\)?
- A. \(I=10\).
- B. \(I=15\).
- C. \(I=-5\).
- D. \(I=20\).
-
Câu 25: Mã câu hỏi: 466366
Cho hàm số bậc 3 \(y=f\left( x \right)\) có đồ thị như hình sau:
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
- A. \(\left( 0\,;\,2 \right)\).
- B. \(\left( -\infty \,;\,-1 \right)\).
- C. \(\left( 2\,;\,4 \right)\).
- D. \(\left( -1\,;\,2 \right)\).
-
Câu 26: Mã câu hỏi: 466368
Cho tập hợp \(M=\left\{ 1;2;3;4;5 \right\}\). Số tập con gồm 2 phần tử của tập hợp \(M\) là?
- A. 11.
- B. \(A_{5}^{2}\).
- C. \(C_{5}^{2}\).
- D. \({{P}_{2}}\).
-
Câu 27: Mã câu hỏi: 466371
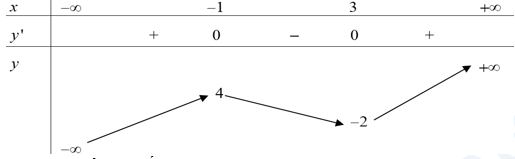
Cho hàm số \(y=f(x)\) có BBT như sau:
Giá trị cực đại của hàm số đã cho là?
- A. \(-1.\)
- B. \(4.\)
- C. \(3.\)
- D. \(-2.\)
-
Câu 28: Mã câu hỏi: 466373
Giả sử \(D\) là hình phẳng giới hạn bởi đường parabol \(y={{x}^{2}}-3x+2\) và trục hoành. Quay \(D\) quanh trục hoành ta thu được khối tròn xoay có thể tích V bằng?
- A. \(V=\frac{\pi }{30}\).
- B. \(V=\frac{1}{6}\).
- C. \(V=\frac{\pi }{6}\).
- D. \(V=\frac{1}{30}\).
-
Câu 29: Mã câu hỏi: 466374
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\), \(BC=a,\ AC=2a,\ {A}'A=a\sqrt{3}\). Tính góc giữa mp \(\left( BCD'A' \right)\) và mp \(\left( ABCD \right)\)?
- A. \(30{}^\circ \).
- B. \(45{}^\circ \).
- C. \(60{}^\circ \).
- D. \(90{}^\circ \).
-
Câu 30: Mã câu hỏi: 466376
Kết quả thu gọn biểu thức sau đây \(P=\ln \left( 4x \right)-\ln \left( 2x \right)\) là?
- A. \(P=\ln \left( 2x \right)\).
- B. \(P=\ln 2\).
- C. \(P=\ln \left( 8x \right).\)
- D. \(P=\ln \left( 8{{x}^{2}} \right)\)
-
Câu 31: Mã câu hỏi: 466378
Cho hàm số bậc 3 \(y=f\left( x \right)\) có đồ thị là đường cong trong hình bên:
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( x \right)+1=m\) có hai nghiệm không âm?
- A. 2
- B. 1
- C. 3
- D. 4
-
Câu 32: Mã câu hỏi: 466380
Thầy Bình đặt lên bàn \(30\) tấm thẻ đánh số từ \(1\) đến \(30\). Bạn An chọn ngẫu nhiên \(10\) tấm thẻ. Tính xác suất để trong \(10\) tấm thẻ lấy ra có \(5\) tấm thẻ mang số lẻ, \(5\) tấm mang số chẵn trong đó chỉ có 1 tấm thẻ mang số chia hết cho \(10\)?
- A. \(\frac{99}{667}\).
- B. \(\frac{8}{11}\).
- C. \(\frac{3}{11}\).
- D. \(\frac{99}{167}\).
-
Câu 33: Mã câu hỏi: 466383
Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| z-i \right|=\left| \left( 1+i \right)z \right|\) là 1 đường tròn, tâm của đường tròn đó có tọa độ là?
- A. \(\left( 1\,;\,1 \right)\).
- B. \(\left( 0\,;\,-1 \right)\).
- C. \(\left( 0\,;\,1 \right)\).
- D. \(\left( -1\,;\,0 \right)\).
-
Câu 34: Mã câu hỏi: 466384
Tích các nghiệm của phương trình sau \(\log _{2}^{2}x-3{{\log }_{2}}x+2=0\) là?
- A. 3
- B. 6
- C. 8
- D. 2
-
Câu 35: Mã câu hỏi: 466385
Cho hàm số bậc bốn \(y=f\left( x \right)\). Hàm số \(y={f}'\left( x \right)\) có đồ thị như hình sau:
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
- A. \(\left( 1\,;\,4 \right)\).
- B. \(\left( -1\,;\,1 \right)\).
- C. \(\left( 0\,;\,3 \right)\).
- D. \(\left( -\infty \,;\,0 \right)\).
-
Câu 36: Mã câu hỏi: 466386
Trong không gian \(Oxyz\), cho 3 điểm \(A\left( 3\,;-1\,\,;2 \right)\), \(B\left( 0\,;\,1\,;\,3 \right)\) và \(C\left( -1;\,1\,;1 \right)\). Đường thẳng đi qua \(C\) và song song với đường thẳng \(AB\) có phương trình là?
- A. \(\frac{x+3}{-1}=\frac{y-2}{1}=\frac{z-1}{1}\).
- B. \(\frac{x-3}{-1}=\frac{y+2}{1}=\frac{z+1}{1}\).
- C. \(\frac{x-1}{-3}=\frac{y+1}{2}=\frac{z+1}{1}\).
- D. \(\frac{x+1}{-3}=\frac{y-1}{2}=\frac{z-1}{1}\).
-
Câu 37: Mã câu hỏi: 466389
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\), \(AB=a\), \(AC=3a\) và \(SA\) vuông góc với mặt phẳng đáy. K/c từ \(C\) đến mặt phẳng \(\left( SAB \right)\) bằng?
- A. \(\sqrt{2}a\).
- B. \(2a\).
- C. \(a\).
- D. \(2\sqrt{2}a\).
-
Câu 38: Mã câu hỏi: 466390
Cho hàm số sau đây \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(F\left( x \right),G\left( x \right),H\left( x \right)\) là ba nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 8 \right)+G\left( 8 \right)+H\left( 8 \right)=4\) và \(F\left( 0 \right)+G\left( 0 \right)+H\left( 0 \right)=1\). Khi đó \(\int\limits_{0}^{2}{f}\left( 4x \right)\text{d}x\) bằng?
- A. 3.
- B. \(\frac{1}{4}\).
- C. 6.
- D. \(\frac{3}{2}\).
-
Câu 39: Mã câu hỏi: 466393
Có tất cả bao nhiêu số nguyên \(x\) thỏa mãn \(\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}\)?
- A. 116.
- B. 58.
- C. 117.
- D. 100.
-
Câu 40: Mã câu hỏi: 466395
Trong không gian với hệ tọa độ \(Oxyz\), cho 3 điểm \(A\left( 2;\,0;\,-1 \right)\), \(B\left( 1;\,-2;\,3 \right)\), \(C\left( 0;\,1;\,2 \right)\). Tìm tọa độ điểm \({O}'\) là điểm đối xứng với gốc tọa độ \(O\) qua mặt phẳng \(\left( ABC \right)\)?
- A. \({O}'\left( 1;\,\frac{1}{2};\,\frac{1}{2} \right)\).
- B. \({O}'\left( 2;\,1;\,1 \right)\).
- C. \({O}'\left( -10;\,-5;\,-5 \right)\).
- D. \({O}'\left( 2;\,\frac{1}{2};\,\frac{1}{2} \right)\).
-
Câu 41: Mã câu hỏi: 466397
Tìm tất cả các giá trị thực của tham số \(m\) sao cho đồ thị hàm số \(y={{x}^{4}}-2m{{x}^{2}}+2{{m}^{4}}-m\) có 3 điểm cực trị đều thuộc các trục toạ độ?
- A. \(m=2\).
- B. \(m=3\).
- C. \(m=\frac{1}{2}\).
- D. \(m=1\).
-
Câu 42: Mã câu hỏi: 466407
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy là tam giác vuông cân đỉnh \(A\), mặt bên là \(BC{C}'{B}'\) hình vuông, k/c giữa \(A{B}'\) và \(C{C}'\) bằng \(a\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) là?
- A. \(\sqrt{2}{{a}^{3}}\).
- B. \(\frac{\sqrt{2}{{a}^{3}}}{3}\).
- C. \({{a}^{3}}\).
- D. \(\frac{\sqrt{2}{{a}^{3}}}{2}\).
-
Câu 43: Mã câu hỏi: 466411
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để trên tập số phức, phương trình \({{z}^{2}}+2mz+{{m}^{2}}-m-2=0\) có 2 nghiệm \({{z}_{1}},\text{ }{{z}_{2}}\) thoả mãn \(\left| {{z}_{1}} \right|\text{+}\left| \text{ }{{z}_{2}} \right|=2\sqrt{10}\)?
- A. 1
- B. 4
- C. 3
- D. 2
-
Câu 44: Mã câu hỏi: 466415
Cho HS \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right)=0\) và \({f}'\left( x \right)\left( 1+{{e}^{f\left( x \right)}} \right)=1+{{e}^{x}},\forall x\in \mathbb{R}.\) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và 2 đường thẳng \(x=1,x=3\)?
- A. 4
- B. 2
- C. 8
- D. 5
-
Câu 45: Mã câu hỏi: 466418
Xét các số phức \(z,\) \(\text{w}\) thỏa mãn \(\left| z \right|=2\) và \(\left| i.\overline{w} \right|=1\). Khi \(\left| iz+w+3-4i \right|\) đạt GTNN, \(\left| z-\text{w} \right|\) bằng?
- A. \(\frac{\sqrt{29}}{5}\).
- B. \(\sqrt{5}\).
- C. \(3\).
- D. \(\frac{\sqrt{221}}{5}\).
-
Câu 46: Mã câu hỏi: 466419
Trong không gian \(Oxyz\), cho điểm \(M\left( 1;0;-2 \right)\) và đường thẳng \(d:\left\{ \begin{align} & x=1-2t \\ & y=t \\ & z=-1-t \\ \end{align} \right.\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và chứa \(d\). Tổng k/c từ điểm \(N\left( -3;-2;1 \right)\) và \(Q\left( -1;3;0 \right)\) đến \(\left( P \right)\) bằng?
- A. \(\frac{8}{\sqrt{5}}\).
- B. \(\frac{4}{\sqrt{5}}\).
- C. \(\frac{12}{\sqrt{5}}\).
- D. \(\frac{5}{\sqrt{5}}\).
-
Câu 47: Mã câu hỏi: 466421
Cho hình trụ có bán kính \(R\) và chiều cao \(\sqrt{3}R\). Hai điểm \(A\), \(B\) lần lượt nằm trên 2 đường tròn đáy sao cho góc giữa \(AB\) và trục \(d\) của hình trụ bằng \(30{}^\circ \). Tính k/c giữa \(AB\) và trục của hình trụ?
- A. \(d\left( AB,d \right)=\frac{R}{2}\).
- B. \(d\left( AB,d \right)=R\).
- C. \(d\left( AB,d \right)=R\sqrt{3}\).
- D. \(d\left( AB,d \right)=\frac{R\sqrt{3}}{2}\).
-
Câu 48: Mã câu hỏi: 466423
Có tất cả bao nhiêu cặp số nguyên\((x,y)\) thỏa mãn \({{2}^{{{x}^{2}}+{{y}^{2}}+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right){{.4}^{x}}\)?
- A. 3
- B. 6
- C. 5
- D. 7
-
Câu 49: Mã câu hỏi: 466424
Có tất cả bao nhiêu giá trị nguyên âm của tham số \(m\) để hàm số\(y=\left| {{x}^{5}}+2{{x}^{4}}-m{{x}^{2}}+3x-20 \right|\) nghịch biến trên \(\left( -\infty ;-2 \right)\)?
- A. 4
- B. 6
- C. 7
- D. 8
-
Câu 50: Mã câu hỏi: 466426
Trong không gian \(Oxyz,\) cho \(A\left( 0;0;1 \right),B\left( 0;0;9 \right),Q\left( 3;4;6 \right)\). Xét các điểm \(M\) thay đổi sao cho tam giác \(ABM\) vuông tại \(M\) và có diện tích lớn nhất. GTNN của độ dài đoạn thẳng \(MQ\) thuộc khoảng nào dưới đây?
- A. \(\left( 4;\,5 \right).\)
- B. \(\left( 3;\,4 \right).\)
- C. \(\left( 2;\,3 \right).\)
- D. \(\left( 1;\,2 \right).\)





.PNG)
.PNG)
.PNG)
.PNG)

