Chúng ta tiếp tục tìm hiểu dạng số 3 của con lắc lò xo là Viết phương trình dao động của con lắc lò xo. Thực ra bài viết phương trình dao động các em đã được học ở bài dao động điều hòa.

Riêng bài viết phương trình dao động của con lắc lò xo, cũng có cách viết phương trình dao động như những cách cũ nhưng có thêm những cái mới mà đề bài sẽ làm khó các em, đôi khi không để ý, các em sẽ làm không được.

PTDĐ: \(x = A.\cos(\omega t + \varphi )\)
+ Tìm A:
\(\cdot \ A = \frac{\ell _{max} - \ell _{min}}{2} = \frac{\ell}{2}\)
Với ℓ: chiều dài quỹ đạo
• Các công thức đã biết ở bài dao động điều hòa
+ Tìm \(\omega\):
\(\cdot \ \omega = 2\pi f = \frac{2 \pi }{T}\)
\(\cdot \ \omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{g}{\Delta l}}\)
+ Tìm \(\varphi\): (Tương tự bài DĐĐH)
* Chú ý: Các xác đinh biên độ A
+ Đưa vật về vị trí lò xo không biến dạng rồi buông \(\rightarrow A = \Delta \ell\)
+ Đưa vật về vị trí lò xo không biến dạng rồi buông ​và truyền cho vận tốc v₀ \(\Rightarrow A = \sqrt{\Delta \ell ^2 + \left ( \frac{v_0}{\omega } \right )^2}\)
+ Từ VTCB đưa vật về vị trí lò xo bị dãn 1 đoạn x₀ rồi buông ⇒ A = ?
• Con lắc lò xo nằm ngang ⇒ A = |x₀|
• Con lắc lò xo treo thẳng đứng
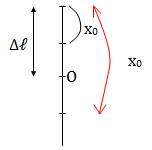\(\Rightarrow A = |x_0 - \Delta \ell|\)
+ Kéo vật ra khỏi vị trí cân bằng 1 đoạn x0  rồi truyền cho vận tốc v0 để vật DĐĐH \(\Rightarrow A = \sqrt{x_{0}^{2} + \left ( \frac{v_0}{\omega } \right )^2}\)

VD1: Một con lắc lò xo treo thẳng đứng gồm 1 lò xo nhẹ có độ cứng k = 40 N/m, vật năng m = 100g. Từ VTCB kéo vật xuống 1 đoạn để lò xo giãn 7,5 cm rồi buông cho vật DĐĐH. Lấy g = 10 m/s². Chọn trục tọa độ Ox trùng với trục lò xo, gốc tọa độ O tại VTCB, chiều dương hướng xuống, gốc thời gian là lúc vật qua VTCB lần đầu tiên. Viết phương trình dao động của vật?
Giải:
m = 100g = 0,1kg
\(\cdot \ \omega \sqrt{\frac{k}{m}} = \sqrt{\frac{40}{0,1}} = 20 \ rad/s\)
\(\cdot \ \Delta \ell = \frac{mg}{k} = \frac{0,1.10}{40} = 0,025\ m\)
\(\rightarrow \Delta \ell = 2,5\ cm\)

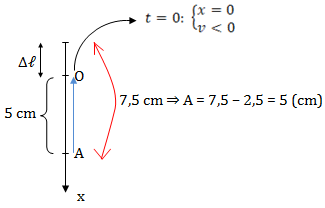
\(t = 0: \left\{\begin{matrix} \cos \varphi = 0\\ \sin \varphi > 0 \end{matrix}\right. \Rightarrow \varphi = \frac{\pi}{2}\)
Vậy \(x = 5\cos (20t + \frac{\pi}{2})\ (cm)\)

VD2: Một con lắc lò xo treo thẳng đứng gồm 1 lò xo có k = 100 N/m, vật nặng m = 100g. Từ VTCB kéo vật xuống 1 đoạn 5 cm rồi truyền cho vật vận tốc \(50 \pi\) cm/s để vật dao động điều hòa. Chọn gốc tọa độ O tại VTCB, trục Ox trùng với trục lò xo. Lấy g = 10 m/s²; \(\pi ^2 = 10\). Chọn gốc thời gian là lúc vật bắt đầu dao động. Viết phương trình dao động của vật?
Giải:
m = 100g = 0,1kg
\(\cdot \ \omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{100}{0,1}} = 10 \pi \ (rad/s)\)
\(\cdot \ \left\{\begin{matrix} |x| = 5 \ cm \ \ \ \ \ \\ v = 50 pi \ cm/s \end{matrix}\right. \Rightarrow A = \sqrt{x^2 + \left ( \frac{v}{\omega } \right )^2}\)
\(\Rightarrow A = \sqrt{5^2 + \left ( \frac{50 \pi} {10 \pi } \right )^2} = 5\sqrt{2} \ cm\)
TH1:
\(t = 0: \left\{\begin{matrix} x = 5 \ \ (Ox \downarrow)\\ v > 0 \hspace{1,5cm}\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \cos \varphi = \frac{1}{\sqrt{2}} \Rightarrow \varphi = \pm \frac{\pi }{4}\\ \sin \varphi < 0 \Rightarrow \varphi = -\frac{\pi}{4} \ \ \end{matrix}\right.\)
Vậy \(x = 5\sqrt{2} \cos (10 \pi t - \frac{\pi }{4})\ (cm)\)
TH2:
\(t = 0: \left\{\begin{matrix} x = -5 \ \ (Ox \uparrow)\\ v > 0 \hspace{1,7cm}\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \cos \varphi = -\frac{1}{\sqrt{2}} \Rightarrow \varphi = \pm \frac{3 \pi }{4}\\ \sin \varphi < 0 \Rightarrow \varphi = -\frac{3 \pi}{4} \ \ \ \ \end{matrix}\right.\)
Vậy \(x = 5\sqrt{2} \cos (10 \pi t - \frac{3\pi }{4})\ (cm)\)