YOMEDIA
Playlist: THPT QG Vật lý - Chuyên đề Sóng cơ...

  • Video liên quan

  • Nội dung

Chúng ta tiếp tục tìm hiểu dạng 3: Gaio thoa với hai nguồn ngược pha hoặc lệch pha một góc \Delta \varphi. Tại sao lại nói ngược pha hoặc lệch pha? Thực tế không chỉ xảy ra mỗi 2 trường hợp này, đề thi từ khi đổi mới hoặc cho  cùng pha hoặc ngược pha, trường hợp lệch pha đề thi chưa cho nhưng không có nghĩa là không cho. Nên ở đây chúng ta sẽ xét trường hợp tổng quát nhất, sau đó coi kết quả ngược lại của trường họp tổng quát thì cùng pha sẽ như thế nào? Ngược pha như thế nào? Lệch pha một góc như thế nào?

Xét 2 nguồn: \left\{\begin{matrix} u_A = a.\cos (\omega t + \varphi _1)\\ u_B = a.\cos (\omega t + \varphi _2) \end{matrix}\right.,\ \Delta \varphi = \varphi _2 - \varphi _1
Điểm M trong vùng giao thoa cách A, B các đoạn d1, d2
\Rightarrow \left\{\begin{matrix} u_{AM} = a.\cos (\omega t + \varphi _1 - \frac{2 \pi d_1}{\lambda })\\ u_{BM} = a.\cos (\omega t + \varphi _2 - \frac{2 \pi d_2}{\lambda }) \end{matrix}\right. \Rightarrow u_M = u_{AM} + u_{BM}
\Rightarrow u_{M} = 2a.\cos \left [ \frac{\lambda }{2}(d_2 - d_1) + \frac{\varphi _1 - \varphi _2}{2} \right ] \times \cos \left [ \omega t + \frac{\varphi _1 + \varphi _2}{2} - \frac{\pi }{\lambda } (d_1 + d_2)\right ]
* Biên độ sóng tại M
A_M = 2a.\left | \cos \left [ \frac{\pi }{\lambda } (d_2 - d_1) - \frac{\Delta \varphi }{2}\right ] \right |
+ Tại M sóng có biên độ cực đại
(A_M)_{max} = 2a \Leftrightarrow \cos \left [ \frac{\pi }{\lambda } (d_2 - d_1) - \frac{\Delta \varphi }{2}\right ] = \pm 1
\Rightarrow \frac{\pi }{\lambda } (d_2 - d_1) - \frac{\Delta \varphi }{2} = k \pi
d_2 - d_1= \left (k + \frac{\Delta \varphi }{2 \pi } \right )\lambda , \ \ \ k \in Z
+ Tại M sóng có biên độ cực tiểu
(A_M)_{min} = 0 \Leftrightarrow \cos \left [ \frac{\pi }{\lambda } (d_2 - d_1) - \frac{\Delta \varphi }{2}\right ] = 0
\Rightarrow \frac{\pi }{\lambda } (d_2 - d_1) - \frac{\Delta \varphi }{2} = \left ( k + \frac{1}{2} \right ) \pi
\Rightarrow d_2 - d_1 = \left ( k + \frac{1}{2} + \frac{\Delta \varphi }{2 \pi }\right ) \lambda , \ \ k \in Z
• Khi uA, uB cùng pha ⇒ \Delta \varphi = 0
\Rightarrow \left\{\begin{matrix} (A_M)_{max} \Rightarrow d_2 - d_1 = k\lambda \hspace{1,1cm} \\ (A_M)_{min} \Rightarrow d_2 - d_1 = \left (k + \frac{1}{2} \right )\lambda \end{matrix}\right.
• Khi uA, uB ngược pha ⇒ \Delta \varphi = \pi
\Rightarrow \left\{\begin{matrix} (A_M)_{max} \Rightarrow d_2 - d_1 = \left (k + \frac{1}{2} \right )\lambda \ \ \ \ \ \ \\ (A_M)_{min} \Rightarrow d_2 - d_1 = (k + 1)\lambda = k' \lambda \end{matrix}\right.
Nhận xét: Khi giao thoa với hai nguồn NGƯỢC PHA thì mọi kết quả ĐẢO NGƯỢC với hai nguồn CÙNG PHA
* Chú ý:
(1) Khi giao thoa với hai nguồn ngược pha thì đường trung trực của đoạn thẳng nối hai nguồn là một đường cực tiểu.
(2) Khi giao thoa với 2 nguồn khác biên độ thì \left\{\begin{matrix} A_{max} = a_1 + a_2\\ A_{min} = |a_1 - a_2| \end{matrix}\right.

VD1: Tại hai điểm S1, S2 cách nhau 20 cm trên mặt nước có hai nguồn dao động với phương trình u_{S_1} = 3 \cos (40 \pi t - \frac{\pi}{3}) (cm) và u_{S_2} = 4 \cos (40 \pi t + \frac{2\pi}{3}) (cm), tốc độ truyền sóng v = 80 cm/s. Tìm số điểm có biên độ 7 (cm) trên S1, S2?
Giải:
\Delta \varphi = \frac{2 \pi }{3} - \left ( -\frac{\pi }{3} \right ) = \pi ⇒ 2 nguồn ngược pha
\omega = 40 \pi \Rightarrow f = \frac{\omega }{2 \pi } = 20\ Hz
\rightarrow \lambda = \frac{v}{f} = 4 \ cm
Hai nguồn ngược pha \Rightarrow \left\{\begin{matrix} A_{max} = 7\ cm \hspace{1,2cm}\\ d_2 - d_1 = \left ( k + \frac{1}{2} \right )\lambda \end{matrix}\right.
\Rightarrow \left | k + \frac{1}{2} \right | < \frac{AB}{\lambda } = \frac{20}{4} = 5 \ cm
\Rightarrow -5 < k + \frac{1}{2} < 5
\Rightarrow -5,5 < k < 4,5 \Rightarrow k = -5; -4; ... ; 3; 4
⇒ Có 4 - (-5) + 1 = 10 giá trị k \in Z
Vậy trên S1, S2 có 10 điểm thỏa yêu cầu bài toán.

VD2: Trên mặt nước tại hao điểm A, B cách nhau 50 cm có 2 nguồn dao động với phương trình u_A = 2\cos (20 \pi t - \frac{\pi }{2}) (cm) và u_B = 2\cos (20 \pi t + \frac{\pi }{2}) (cm). Xét điểm C trong vùng giao thoa sao cho tam giác ABC vuông cân tại A. Tốc độ truyền sóng v = 50 cm/s. Tìm số điểm cực đại trên trung tuyến CI?
Giải:
f = \frac{\omega }{2 \pi } = \frac{20 \pi }{2 \pi } = 10 \ Hz
\rightarrow \lambda = \frac{v}{f} = \frac{50}{10} = 5 \ cm

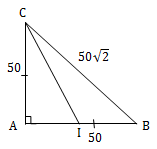
Hai nguồn ngược pha \Rightarrow \left\{\begin{matrix} A_{max} \hspace{2,6cm}\\ d_2 - d_1 = \left ( k + \frac{1}{2} \right )\lambda \end{matrix}\right.
• Xét |CB - CA| = 50\sqrt{2} - 50
• Xét |IB- IA| = 0
\Rightarrow |IB - IA| \leq \left ( k + \frac{1}{2} \right )\lambda \leq |CB - CA|
\Rightarrow \frac{0}{5} \leq k + \frac{1}{2} \leq \frac{50\sqrt{2} - 50}{5} \Rightarrow -\frac{1}{2} \leq k \leq 3,6
⇒ k = 0; 1; 2; 3 ⇒ Có 4 giá trị k.
⇒ Trên CI có 4 điểm thỏa yêu cầu bài toán.

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

ATNETWORK
ON