Chúng ta xét, Điện thế cực đại của quả cầu cô lập về điện, quả cầu làm bằng kim loại, cô lập là không trao đổi điện tích với bên ngoài. Riêng dạng bài tập này liên quan đến kiến thức lớp 11. Nếu đề thi cho dạng bài tập này thì không phải quá khó, nhưng hiện tượng xảy ra các em không hiểu hoặc quên, thực ra công thức ở đây chúng ta áp dụng các công thức rất đơn giản.

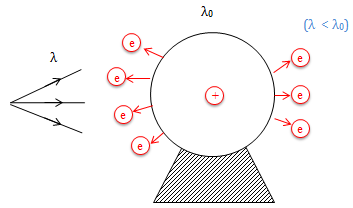
Chiếu áng sáng đơn sắc có bước sóng \(\lambda\) thích hợp vào quả cầu kim loại đặt cô lập về điện ⇒ Các phôtôn của ánh sáng làm bứt các electron quang điện ra khỏi quả cầu ⇒ Quả cầu tích điện dương ⇒ Xung quanh quả cầu xuất hiện 1 điện trường cản trở chuyển động của electron ⇒ Khi lực điện trường đủ lớn thì các quang electron vừa bứt ra khỏi quả cầu sẽ bị hút ngược trở lại (vẫn xảy ra hiện tượng quang điện) ⇒ Khi đó điện thế của quả cầu đạt cực đại ⇒ |e|.V_max = E_{đo max}
Theo công thức Anhxtanh
\(\frac{hc}{\lambda }\) = A + E_{đo max}
⇒ E_{đo max} = \(\frac{hc}{\lambda }\) - A =  |e|.V_max 
\(\Leftrightarrow \frac{1}{2}mv_{0\ max}^{2} = |e|V_{max}\)

VD1: Chiếu một bức xạ có \(\lambda = 0,14\ \mu m\) vào một quả cầu bằng đồng có công thoát A = 4,57eV đặt cô lập về điện. Tìm điện thế cực đại của quả cầu?
Giải:
• A = 4,57eV = 4,57.16.10^-19 = 7,312.10^-19 J
• Giới hạn quang điện: \(\lambda _0 = \frac{hc}{A}\)
\(\Rightarrow \lambda _0 = \frac{6,625.10^{-34}.3.10^8}{7,312.10^{-19}} = 0,27\ \mu m\)
\(\lambda = 0,14 \ \mu m < \lambda _0 = 0,27\ \mu m\)
Ta có: |e|.V_max = E_{đo max} = \(\frac{hc}{\lambda }\) - A
\(\Rightarrow V_{max} = \left ( \frac{hc}{\lambda } - A \right ).\frac{1}{|e|} = \left ( \frac{6,625.10^{-34}.3.10^8}{0,14.10^{-6}}- 7,312.10^{-19} \right ).\frac{1}{1,6.10^{-19}}\)
\(\Rightarrow V_{max} = 4,3\ (V)\)

VD2: Chiếu một chùm sóng gồm 2 bức xạ đơn sắc có bước sóng \(\lambda _1,\ \lambda _2\) vào 1 quả cầu kim loại có giới hạn quang điện \(\lambda _0\) (với \(\lambda _1 < \lambda _2 < \lambda _0\)). Tìm điện thế cực đại của quả cầu?
Giải:
\(\lambda _1 < \lambda _2 \Rightarrow \varepsilon _1 > \varepsilon _2 \Rightarrow V_{1\ max} > V_{2\ max}\)
\(\Rightarrow V_{max} = V_{1\ max}\)
\(\Rightarrow |e|.V_{max} =\) E_{đo max} \(= \frac{hc}{\lambda _1} - A\)
\(\Rightarrow |e|.V_{max} = \frac{hc}{\lambda _1} - \frac{hc}{\lambda _0}\)
\(\Rightarrow V_{max} = \frac{hc}{|e|} \left ( \frac{1}{\lambda _1} - \frac{1}{\lambda _0} \right )\)