Bữa trước chúng ta đã học lý thuyết về Dao động tắt dần - Dao động duy trì - Dao động cưỡng bức - Sự cộng hưởng. Hôm nay chúng ta tìm hiểu dạng bài tập đầu tiên đó là Dao động cưỡng bức - Sự cộng hưởng.

Dạng bài tập này thực ra rất dễ, rất đơn giản nhưng khi cho vào đề thi, một số học sinh không hiểu đề đang nói vấn đề gì? Vì thế các em cần chú ý, coi lại lý thuyết dao động cưỡng bức là gì? Có những tính chất, đặc điểm gì? Biên độ phụ thuộc vào những yếu tố nào? Và thực hành làm lại các bài tập.

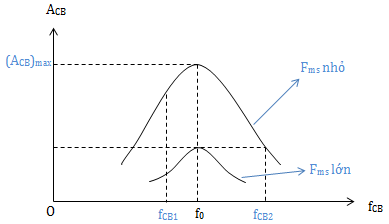
* Dao động cưỡng bức
+ Chịu tác dụng của ngoại lực
\(F_n= F_0 \ cos (2 \pi f_{CB}t + \varphi )\)
+ A_CB tỉ lệ với F₀
+ A_CB phụ thuộc vào |f_CB - f_riêng|
• VD: 
Con lắc lò xo ⇒  f_riêng = f₀ = \(\frac{1}{2\pi}\sqrt{\frac{k}{m}}\)
Con lắc đơn ⇒  f_riêng = f₀ = \(\frac{1}{2\pi}\sqrt{\frac{g}{\ell}}\)
• |f₀ - f_CB| càng lớn thì A_CB càng nhỏ.
• f =  f_CB

* Sự cộng hưởng
A_CB đạt giá trị lớn nhất
Khi f_CB = f₀ 

VD1: Một con lắc đơn có chiều dài ℓ = 1 m, đặt tại nơi có \(g = \pi ^2\) m/s². Tác dụng vào con lắc đơn này một ngoại lực tuần hoàn có biên độ không đổi còn tần số thay đổi được. Nếu tần số của ngoại lực tăng từ 1 Hz đến 2 Hz thì biên độ của con lắc đơn này thay đổi như thế nào?
Giải:
Tần số riêng: \(f_0 = \frac{1}{2 \pi }\sqrt{\frac{g}{\ell}} = \frac{1}{2 \pi }\sqrt{\frac{\pi ^2}{1}} = \frac{1}{2}\ Hz\)
\(f_{CB_{1}} = 1 \ Hz\)
\(f_{CB_{2}} = 2 \ Hz\)
Ta có:
\(|f_{CB_{1}} -f_0|= \left |1- \frac{1}{2} \right | = \frac{1}{2}\)
\(|f_{CB_{2}} -f_0|= \left |2- \frac{1}{2} \right | = \frac{3}{2}\)
\(\Rightarrow |f_{CB_{1}} -f_0| < |f_{CB_{2}} -f_0|\)
\(\Rightarrow A_{CB_{1}} > A_{CB_{2}\)
⇒ Biên độ của con lắc đơn luôn giảm.

VD2: Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k = 10 N/m và vật có khối lượng m. Tác dụng vào con lắc lò xo này một ngoại lực tuần hoàn có biên độ không đổi và \(\omega _{CB}\) thay đổi được. Khi \(\omega _{CB} = 10 \ rad/s\) thì biên độ của con lắc lò xo đạt cực đại. Tìm m?
Giải:
Khi \(\omega _{CB} = 10 \ rad/s\) thì biên độ của con lắc lò xo lớn nhất ⇒ Xảy ra cộng hưởng
\((A_{CB})_{max} \Leftrightarrow \omega _{CB} = \omega _0\)
\(\Rightarrow 10 = \sqrt{\frac{k}{m}} = \sqrt{\frac{10}{m}}\)
\(\Rightarrow 10^2 = \frac{10}{m} \Rightarrow m = 0,1\ kg = 100\ g\)