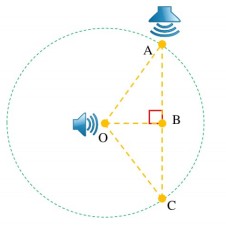
Trong một môi trường đẳng hướng và không hấp thụ âm có 3 điểm thẳng hàng theo đúng thứ tự A,B,C

Cường độ âm tại một điểm cách nguồn một khoảng R được tính bằng công thức: $I = \frac{P}{4 \pi R^2}$

Sóng âm do nguồn âm phát ra là sóng cầu (sóng truyền theo mọi hướng và có mặt đầu sóng hình cầu)

Mức cường độ âm tại A và C bằng nhau suy ra: OA = OC → tam giác $\Delta OAC$ cân tại O

Vì B nằm trên AC và có  mức cường độ âm lớn nhất nhên B phải gần O nhất

$\rightarrow$ OB là đường cao của tam giác $\Delta OAC$ như hình vẽ

Ta có: $L_B - L_A = 10 lg \frac{I_B}{I_A} = 10 lg \frac{OA^2}{OB^2} = 46,02 - 40$

$\Rightarrow \frac{OA^2}{OB^2}= 10^{0,602}\Rightarrow OA^2 = 10^{0,602}OB^2$

Từ hình vẽ ta có: $AB^2 = OA^2 - OB^2 = (10^{0.602 }- 1)OB^2$

Khi đặt nguồn p' tại A, để mức cường độ âm tại B không đổi thì cường độ âm tại B củng không đổi, Ta có:
$I = \frac{P}{4 \pi OB^2} = \frac{P' }{4 \pi AB^2}\Rightarrow P' = \frac{AB^2}{0B^2}P = \frac{(10^{0.602} - 1)OB^2}{OB^2}P \Leftrightarrow P' \approx 3P$