-
Câu hỏi:
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.\) Gọi \(A,\,\,B\) là hai điểm trên mặt cầu \(\left( S \right)\) và \(AB=4;\) \({A}',\,\,{B}'\) là hai điểm nằm trên mặt phẳng \(\left( P \right)\) sao cho \(A{A}',\,\,B{B}'\) cùng song song với đường thẳng \(d.\) Giá trị lớn nhất của tổng \(A{A}'+\,B{B}'\) gần nhất với giá trị nào sau đây
- A. \(13.\)
- B. \(11.\)
- C. \(12.\)
- D. \(14.\)
Lời giải tham khảo:
Đáp án đúng: D
Chọn D
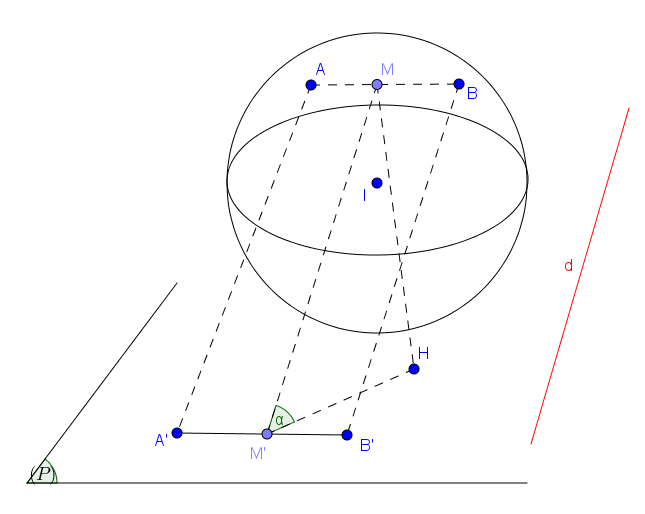
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 1;0;2 \right)\) và bán kính \(R=\sqrt{5}\).
\(d\left( I;\left( P \right) \right)\)\( =\frac{10\sqrt{3}}{3}>R\) nên \((P)\) và mặt cầu \((S)\) không giao nhau.
Gọi \(M\) là trung điểm của \(AB\), \({M}'\) là trung điểm của \(A\prime B\prime \) thì \(AA\prime +BB\prime =2M{M}'\)\( =2.\frac{MH}{\sin \left( M;\left( P \right) \right)}\).
Khi đó \(M{{H}_{\max }}\)\( =\sqrt{{{R}^{2}}-\frac{A{{B}^{2}}}{4}}+d\left( I;\left( P \right) \right)=\sqrt{5-4}+\frac{10\sqrt{3}}{3}\)\( =\frac{3+10\sqrt{3}}{3}\).
Ta có \(\sin \left( M;\left( P \right) \right)\)\( =\sin \left( d;\left( P \right) \right)\)\( =\frac{5\sqrt{3}}{9}\).
Vậy \({{\left( A{A}'+\,B{B}' \right)}_{\max }}\)\( =2.\frac{\frac{3+10\sqrt{3}}{3}}{\frac{5\sqrt{3}}{9}}\)\( =\frac{60+6\sqrt{3}}{5}\approx 14,08\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Nghiệm của phương trình \({{2023}^{x-1}}=1\) là
- Cho hình nón có diện tích xung quanh bằng \(8\pi \) và độ dài đường sinh là \(4\)
- Số điểm cực trị của hàm số \(y=-{{x}^{4}}-4{{x}^{3}}+3\) là
- Tập nghiệm của bất phương trình \({{\log }_{2}}\left( x-2 \right)
- Cấp số nhân \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=1\)
- Đồ thị hàm số nào dưới đây có dạng của hình bên?
- Trong không gian với hệ tọa độ \(Oxyz\), điểm \(M'\)đối xứng với điểm
- Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn
- Cho đồ thị hàm số \(y=\frac{x}{x-2}\). Khẳng định nào sau đây đúng?
- Trong không gian với hệ tọa độ \(Oxyz\), phương trình mặt phẳng
- Trong không gian với hệ tọa độ \(Oxyz\), vectơ
- Số phức liên hợp của số phức \(1-3i\) là
- Cho hàm số \(y={{x}^{3}}+x+1\). Giá trị lớn nhất của hàm số trên đoạn
- Tìm tập xác định của hàm số \(y=\ln \left( -{{x}^{2}}+4 \right)\).
- Trong các hàm số sau đây, hàm số nào là nguyên hàm của hàm số
- Cho khối trụ \(\left( T \right)\) có bán kính đáy bằng \(2\) và chiều cao bằng \(4\)
- Thể tích của khối lăng trụ tam giác đều tất cả các cạnh bằng \(2\) là
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
- Số giá trị nguyên của tham số \(m\) để hàm số \(y={{x}^{3}}-3m{{x}^{2}}+3x+1\)
- Cho hình chóp \(S.ABC\) có \({A}',\,\,{B}'\) lần lượt là trung điểm của \(SA,\,\,SB\)
- Cho \(M\) là giao điểm của đồ thị hàm số \(y=\frac{x+1}{x-2}\) với trục hoành
- Với \(a,b\) là các số thực dương bất kì, \({{\log }_{2}}\left( a{{b}^{3}} \right)\) bằng:
- Một túi đựng 5 bi xanh và 5 bi đỏ. Lấy ngẫu nhiên 2 bi
- Tổng hai nghiệm của phương trình \({{2}^{{{x}^{2}}+x+1}}={{8}^{2x}}\)
- Số nghiệm nguyên của bất phương trình
- Trong không gian với hệ tọa độ \(Oxyz\), đường thẳng \(d\) đi qua điểm
- Cho số phức \(z=1+i\). Môđun của số phức \(w=\left( 1+3i \right)z\) là
- Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn
- Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\frac{x-2}{1}=\frac{y+2}{2}=\frac{z}{-2}\) và mặt phẳng
- Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị \(\left( P \right):y=2x-{{x}^{2}}\)
- Thể tích khối cầu nội tiếp hình lập phương cạnh \(2a\) là
- Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh
- Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\)
- Tìm \(a\) để đồ thị hàm số \(y={{\log }_{a}}x\left( 0
- Trong không gian, cho hình chữ nhật \(ABCD\) có \(AB=2\),\(AD=1\)
- Có bao nhiêu số nguyên \(x\) thỏa mãn \(\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}\)?
- Trong không gian \(Oxyz\), cho điểm \(M\left( -1;1;3 \right)\) và hai đường thẳng \(\Delta :\frac{x-1}{3}=\frac{y+3}{2}=\frac{z-1}{1}\), \({\Delta }':\frac{x+1}{1}=\frac{y}{3}=\frac{z}{-2}\)
- Cho lăng trụ đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a\)
- Cho hàm số\(y=f\left( x \right)\)xác định \(R\backslash \left\{ 0 \right\}\) thoả mãn
- Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số
- Trên tập hợp các số phức, xét phương trình \({{z}^{2}}-2\left( m+1 \right)z+{{m}^{2}}=0\) (\(m\) là tham số thực).
- Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ -5;\,3 \right]\)
- Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\)
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật
- Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\)
- Cho hình nón đỉnh \(S,\) đáy là hình tròn tâm \(O,\) góc ở đỉnh của hình nón
- Cho hai số phức \({{z}_{1}},\,\,{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}+2-i \right|+\left| {{z}_{1}}-4-7i \right|
- Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\)
- Có bao nhiêu giá trị nguyên của tham số \(m\) để tập nghiệm của bất phương trình
- Cho hàm số \(f(x)={{\ln }^{3}}x+6(m-1){{\ln }^{2}}x-3{{m}^{2}}\ln x+4\).







