Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất

Áp dụng kết quả bài toán điều kiện để một vị trí cực đại và cùng pha với nguồn

 \(\left\{ \begin{array}{l} {d_2} - {d_1} = k\lambda \\ {d_2} + {d_1} = n\lambda \end{array} \right.\left( 1 \right)\)  với n, k cùng chẵn hoặc cùng lẽ

+ Số dãy dao động với biên độ cực đại:

\(- \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow - \frac{{18}}{5} < k < \frac{{18}}{5} \Leftrightarrow - 3,6 < k < 3,6\)

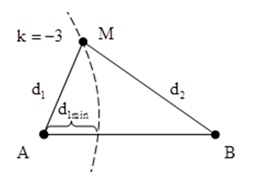
+ Để M gần A nhất thì khi đó M phải nằm trên cực đại ứng với k=-3 , áp dụng kết quả ta có:  

\(\left\{ \begin{array}{l} {d_2} - {d_1} = 3\lambda \\ {d_2} + {d_1} = n\lambda \end{array} \right. \Leftrightarrow n = 3 + \frac{{2{{\rm{d}}_1}}}{\lambda }\)  chú ý rằng n là một số lẻ

+ Mặc khác từ hình vẽ ta có thể xác định được giá trị nhỏ nhất của d₁ như sau

\(\left\{ \begin{array}{l} {d_2} - {d_{1\min }} = 15\\ {d_2} + {d_{1in}} = 18 \end{array} \right. \Leftrightarrow 2{{\rm{d}}_{1\min }} = 3\)

Thay vào biểu thức trên ta thu được   \(n \ge 3 + \frac{{2{{\rm{d}}_{1\min }}}}{\lambda } = 3 + \frac{3}{5} = 3,6\)

Vậy số lẻ gần nhất ứng với n=5 

Thay trở lại phương trình (1) ta tìm được  d₁ =5cm