Ở mặt nước, tại hai điểm S1 và S2 có hai nguồn dao động cùng pha theo phương thẳng đứng

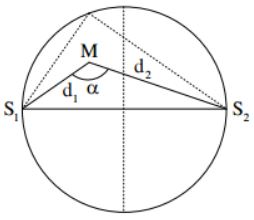
Gọi M là môt điểm bất kì trên nửa phía trên.

- Để tại M các phần tử nước dao động với biên độ cực đại và cùng pha với nguồn sóng do hai nguồn truyền tới M phải cùng pha với nhau và cùng pha với nguồn, suy ra M phải cách các nguồn một số nguyên lần bước sóng.

\(\left\{ {\begin{array}{*{20}{c}} {{d_1} = {k_1}\lambda }\\ {{d_2} = {k_2}\lambda } \end{array}} \right.\)

Để M nằm bên trong đường tròn (C) thì  \(\alpha > {90^0}\)\(\Rightarrow \cos \alpha < 0\)  

Áp dụng định lý hàm cos cho tam giác \(M{S_1}{S_2}\)  ta có:  

\(\cos \alpha = \frac{{d_1^2 + d_2^2 - {{\left( {{S_1}{S_2}} \right)}^2}}}{{2{d_1}{d_2}}} = \frac{{k_1^2 + k_2^2 - 5,{4^2}}}{{2{k_1}{k_2}}}\)

\(\cos \alpha < 0 \Rightarrow k_1^2 + k_2^2 < 5,{4^2} = 29,16\)

\(\Rightarrow \left| {{d_1} - {d_2}} \right| < {S_1}{S_2} < {d_1} + {d_2} \Rightarrow \left| {{k_1} - {k_2}} \right| < 5,4 \le {k_1} + {k_2}\)

Vậy có tất cả 9 điểm  tính thêm nửa dưới ta có 18 điểm.