-
Câu hỏi:
Một cái chuông có dạng như hình vẽ. Giả sử khi cắt chuông bởi mặt phẳng qua trục của chuông, được thiết diện có đường viền là một phần parabol (hình vẽ). Biết chuông cao 4m, và bán kính của miệng chuông là \(2\sqrt 2 \). Tính thể tích chuông?
.png)
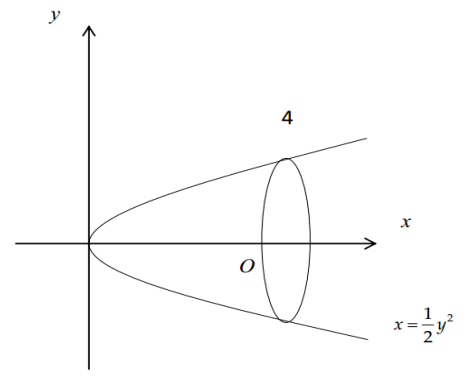
Xét hệ trục như hình vẽ, dễ thấy parabol đi qua ba điểm \(\left( {0;0} \right),\left( {4;2\sqrt 2 } \right),\left( {4; - 2\sqrt 2 } \right)\) nên có phương trình \(x = \frac{{{y^2}}}{2}\).
Thể tích của chuông là thể tích của khối tròn xoay tạo bởi hình phẳng \(y = \sqrt {2 x},x = 0,x = 4\) quay quanh trục Ox.
Ta có \(V = \pi \int\limits_0^4 {2xdx} = \left. {\left( {\pi {x^2}} \right)} \right|_0^4 = 16\pi \)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ ỨNG DỤNG CỦA TÍCH PHÂN VÀ NGUYÊN HÀM
- Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=ax^3(a>0), trục hoành và hai đường thẳng x=−1, x=k (k>0) bằng 17a/4.
- Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD với A(−1;2), B(5;5), C(5;0), D(−1;0). Quay hình thang ABCD xung quanh trục Ox thì thể tích khối nón tròn xoay tạo thành là bao nhiêu?
- Cho mặt phẳng (H) giới hạn bởi đồ thị hàm số y = sqrt x ,y = x - 2 và trục hoành. Tìm công thức tính thể tích của vật thể tròn xoay sinh ra khi cho hình (H) quay quanh trục hoành.
- Phần trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn cách nhau 4m
- Từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc v(t)=−5t+a(m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.
- Tính diện tích S của hình phẳng giới hạn bởi các đường y = sqrt x ,y = {x^3}.
- Tính diện tích S của hình phẳng giới hạn bởi các đường y=1,y=1/9(6x^2−x^4).
- Tính thể tích của khối tròn xoay được tạo thành khi quay hình phẳng được giới hạn bởi y = 2 - {x^2};y = 1
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2x+1/x-2 tiệm cận ngang và hai đường thẳng
- Một vật chuyển động chậm dần với vận tốc vleft( t ight) = 160 - 10t,left( {m/s} ight).






