Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I. Biết AB=20cm, AC=28cm, BC=24cm. Khi đó IA bằng bao nhiêu cm?

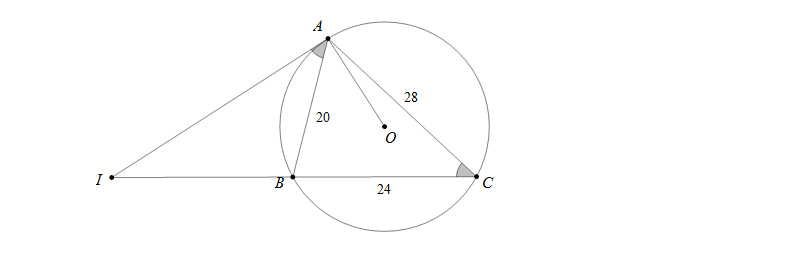
Đặt \(IA=x, IC=y\). Ta có \(\bigtriangleup BAI \sim \bigtriangleup ACI\) (g.g) \(\Rightarrow \frac{AI}{CI}=\frac{BI}{AI}=\frac{AB}{CA}\)

Suy ra  \(\frac{x}{y}=\frac{y-24}{x}=\frac{20}{28}=\frac{5}{7}\)

Từ đây ta có hệ  \(\left\{\begin{array}{l} 7x=5y \\ 5x=7(y-24) \end{array}\right.\Rightarrow \left\{\begin{array}{l} x=35 \\ y=49 \end{array}\right.\)

Khi đó IA=35cm.