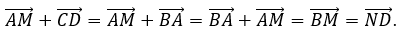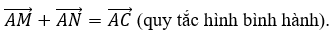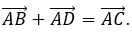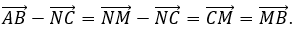-
Câu hỏi:
Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Cặp vectơ nào trong số các cặp vectơ sau đây không bằng nhau?
- A. \(\overrightarrow {NC} + \overrightarrow {MC} \) và \(\overrightarrow {AD} \)
- B. \(\overrightarrow {AM} + \overrightarrow {CD} \) và \(\overrightarrow {ND} \)
- C. \(\overrightarrow {AB} - \overrightarrow {NC} \) và \(\overrightarrow {MB} \)
- D. \(\overrightarrow {AM} + \overrightarrow {AN} \) và \(\overrightarrow {AB} + \overrightarrow {AD} \)
Lời giải tham khảo:
Đáp án đúng: A
Vì \(\overrightarrow {MC} = \overrightarrow {AN} \)
Ta có \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {AN} = \overrightarrow {AN} + \overrightarrow {NC} = \overrightarrow {AC} \ne \overrightarrow {AD} \)
Chọn A.
Lưu ý: Trong phương án B, vì CD→=BA→, ta có
Trong phương án D, vì tứ giác AMCN là hình bình hành nên ta có:
Vì tứ giác ABCD là hình bình hành nên
Suy ra
Trong phương án C,
Chọn A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Vectơ tổng hợp của hai vectơ như hình vẽ sau có độ lớn là? (giả sử ô vuông có đơn vị là cm)
- Vectơ tổng hợp của hai vectơ trong hình sau có độ lớn là?
- Cho 2 điểm phân biệt A và B. Tập hợp các điểm O thỏa mãn vec{OA}=vec{OB} là:
- Vectơ đối của tổng sau vec{a}+vec{b}-vec{c} là:
- Cho tam giác ABC vuông tại A có \(AB = \sqrt 5 ,AC = 2\sqrt 5 \). Độ dài vectơ AB→ + AC→ bằng:
- Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD.
- Cho tam giác ABC. Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá trị chứa đường thẳng nào sau đây?
- Cho tam giác ABC vuông tại A và AB = 3, AC = 8. Vectơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài là:
- Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.
- Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây?




.PNG)