-
Câu hỏi:
Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
- A. \(4<m\le 8\)
- B. \(0<m\le 2\)
- C. \(2<m\le 4\)
- D. \(m>8\).
Lời giải tham khảo:
Đáp án đúng: C
Ta có \(y'=m-\frac{36}{{{\left( x+1 \right)}^{2}}}.\)
* Với \(m\le 0,\) hàm số nghịch biến trên \(\left[ 0;3 \right]\) nên \(\underset{x\in \left[ 0;3 \right]}{\mathop{\min }}\,y=y\left( 3 \right)=3m+9\)
Suy ra \(3m+9=20\Leftrightarrow m=\frac{11}{3}\) (không thỏa mãn)
* Với \(m>0,\) ta có:
\(y'=\frac{m{{\left( x+1 \right)}^{2}}-36}{{{\left( x+1 \right)}^{2}}}.\\ y'=0\Leftrightarrow x+1=\pm \frac{6}{\sqrt{m}}\\\Leftrightarrow \left[ \begin{align} & x=-1+\frac{6}{\sqrt{m}} \\ & x=-1-\frac{6}{\sqrt{m}}\left( L \right) \\ \end{align} \right.\)
- Khi \(0\le -1+\frac{6}{\sqrt{m}}\le 3\Leftrightarrow \frac{9}{4}\le m\le 36,\) ta có bảng biến thiên của hàm số:
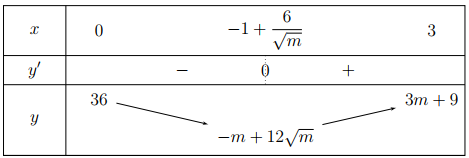
Dựa vào bảng biến thiên ta suy ra
\(\underset{x\in \left[ 0;3 \right]}{\mathop{\min }}\,y=y\left( -1+\frac{6}{\sqrt{m}} \right)=-m+12\sqrt{m}=20\\\Leftrightarrow \left[ \begin{align} & m=4 \\ & m=100\left( L \right) \\ \end{align} \right..\)
- Khi \(-1+\frac{6}{\sqrt{m}}>3\Leftrightarrow m<\frac{9}{4},\) ta có bảng biến thiên của hàm số:
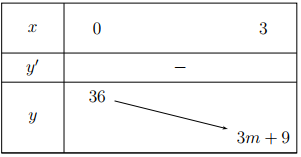
Dựa vào bảng biến thiên ta suy ra \(\underset{x\in \left[ 0;3 \right]}{\mathop{\min }}\,y=y\left( 3 \right)=3m+9=20\Leftrightarrow m=\frac{11}{9}\) (loại).
Vậy giá trị nhỏ nhất bằng 20 khi \(m=4.\)
Chọn đáp án C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Hàm số nghịch biến trên khoảng nào dưới đây?
- Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong hình bên. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng
- Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}.\) Mệnh đề nào sau đây là mệnh đề đúng?
- Hàm số nào sau đây đồng biến trên \(\left( { - \infty ;+ \infty} \right)\)
- Hàm số \( y=x^4+x^2-2\) nghịch biến trên khoảng nào trong các khoảng sau?
- Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của hàm số \(y = f'\left( x \right)\) như hình dưới đây.
- Có bao nhiêu cách chọn 2 HS từ một nhóm gồm 34 học sinh?
- Cho hàm số \(y=\frac{2x+1}{x-1}.\) Điểm nào sau đây thuộc đồ thị hàm số?
- Cho cấp số nhân \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=5\) và công bộ \(q=2.\) Giá trị \({{u}_{2}}\) bằng
- Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hàm số đã cho có bao nhiêu điểm cực trị?
- Điểm nào sau đây là điểm cực tiểu của đồ thị hàm số \(y={{x}^{3}}-3x+1\)?
- Cho hàm số \(y={{x}^{3}}+2\). Hàm số có bao nhiêu điểm cực trị?
- Giá trị lớn nhất của hàm số \(f\left( x \right)={{x}^{3}}-3x\) trên đoạn \(\left[ -3;3 \right]\) bằng
- Tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x+3}\) bằng
- Cho hàm số \(y=f\left( x \right)\) có tập xác định \(R\backslash \left\{ -1 \right\},\) có bảng biến thiên như hình vẽ. Đồ thị hàm số có tất cả bao nhiêu tiệm cân đứng và tiệm cận ngang?
- Đồ thị hàm số \(y=\frac{{{x}^{2}}-5x+4}{x-2}\) cắt trục hoành tại bao nhiêu điểm?
- Thể tích của khối lăng trụ có chiều cao bằng \(h\) và diện tích đáy bằng \(B\) là
- Một hình chóp có chiều cao bằng 10cm và diện tích đáy \(30c{{m}^{2}}\) thì có thể tích bằng
- Giá trị nhỏ nhất của hàm số \(y=\frac{3x+1}{x-2}\) trên \(\left[ -1;1 \right]\) bằng
- Cho khối chóp \(S.ABCD\) có đáy \(ABCD\). là hình vuông cạnh bằng \(a,\) cạnh bên \(SA\). vuông góc với mặt đáy và \(SA=3a.\) Thể tích của khối chóp \(S.ABCD\) bằng
- Hình đa diện bên có tất cả bao nhiêu mặt?
- ho hàm số có bảng biến thiên như hình vẽ bên. Đặt \(\mathop {\min }\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=m,\mathop {\max}\limits_{x \in \left[ { - 2;2} \right]}\,f\left( x \right)=M.\) Khẳng định nào dưới đây đúng?
- Cho hàm số \(y=f\left( x \right)\) có \(\underset{x\to +\infty }{\mathop{\lim }}\,y=1\) và \(\underset{x\to -\infty }{\mathop{\lim }}\,y=-1.\) Khẳng định nào sau đây là khẳng định đúng?
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau. Mệnh đề nào sau đây SAI?
- Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. \(y={{x}^{4}}-2x+1\).
- Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị trong hình bên. Số nghiệm của phương trình \(f\left( x \right)=1\) là
- Giá trị cực tiểu của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+2\) là.
- Đường thẳng \(y=2x+1\) cắt đồ thị hàm số \(y={{x}^{3}}+3{{x}^{2}}+4x-5\) tại
- Diện tích ba mặt của hình hộp chữ nhật lần lượt là \(15c{{m}^{2}},24c{{m}^{2}},40c{{m}^{2}}.\) Thể tích của khối hộp đó là
- Cho hàm số \(y=-2{{x}^{3}}+6{{x}^{2}}-5\) có đồ thị \(\left( C \right).\) Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) có hoành độ bằng 3 là
- Cho hàm số \(f\left( x \right)=\left\{ \begin{align} & -{{x}^{2}}+2x\text{ voi }x
- Tính thể tích \(V\) của khối lăng trụ tam giác đều có tất cả các cạnh bằng a
- Cho khối chóp \(S.ABC\). Gọi \(M,N\) lần lượt là trung điểm \(SA\) và \(SB.\) Tính tỉ số thể tích của hai khối chóp \(S.MNC\) và \(S.ABC\).
- Cho khối chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(2a,\) mặt bên \(SAB\) vuông góc với mặt đáy. Tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( SAB \right).\)
- Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) và mặt bên \(ABB'A'\) là hình vuông cạnh bằng \(a\) (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng \(BC'\) và mặt phẳng \(\left( ABB'A' \right).\)
- Cho hàm số \(y={{x}^{3}}-m{{x}^{2}}+2x+1\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số đồng biến trên tập số thực \(R\)?
- Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích bằng 48. Gọi \(M\) là trung điểm của cạnh \(AB.\) Tính thể tích \(V\) của khối tứ diện \(SMCD.\)
- Cho hàm số \(y=\frac{x+1}{x-m},\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( 2;+\infty \right)?\)
- Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(C,AB=a\sqrt{3},AC=2,SC=a\sqrt{5}.\) Hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAC \right)\) cùng vuông góc với mặt phẳng \(\left( ABC \right).\) Thể tích của khối chóp \(S.ABC\) bằng
- Một hộp chứ 7 viên bi đỏ, 8 viên bi trắng, 6 viên bi vàng. Lấy ngẫu nhiên trong hộp ra 4 viên bi. Tính xác suất để chọn được 4 viên bi trong đó có nhiều nhất 2 viên bi vàng.
- Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ. Xét dấu của \(a,b,c.\)
- Biết rằng giá trị nhỏ nhất của hàm số \(y=mx+\frac{36}{x+1}\) trên \(\left[ 0;3 \right]\) bằng 20. Mệnh đề nào sau đây đúng?
- Cho hàm bậc ba \(f\left( x \right)\) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(g\left( x \right)=\frac{1}{f\left( x \right)-2}\) là
- Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng \(200{{m}^{3}}\) đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công cây bể là 300.000 đồng/\({{m}^{2}}\). Chi phí xây dựng thấp nhất là
- Một chất điểm chuyển động theo quy luật \(s\left( t \right)={{t}^{2}}-\frac{1}{6}{{t}^{3}}\left( m \right).\) Tìm thời điểm \(t\) (giây) mà tạo đó vận tốc \(v\left( m/s \right)\) của chuyển động đạt giá trị lớn nhất.
- Cho hàm số \(y=f\left( x \right).\) Hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( {{x}^{3}}+1 \right)\) nghịch biến trên khoảng
- Cho lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có \(AC=4a.\) Gọi \(O\) là tâm của mặt \(A'B'C'D'.\) Biết rằng hai mặt phẳng \(\left( OAB \right)\) và \(\left( OCD \right)\) vuông góc với nhau. Thể tích khối lăng trụ \(ABCD.A'B'C'D'\) bằng
- Cho khối chóp \(S.ABC\) có \(AB\bot BC,BC\bot SC,SC\bot SA,BC=a,SC=\sqrt{15}a\) và góc giữa \(AB,SC\) bằng \({{30}^{0}}.\) Thể tích khối chóp \(S.ABC\) bằng
- Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( \sqrt[3]{f\left( x \right)+m} \right)={{x}^{3}}-m\) có nghiệm \(x\in \left[ 1;2 \right]\) biết \(f\left( x \right)={{x}^{5}}+3{{x}^{3}}-4m.\)
- Cho hàm số \(y=f\left( x \right)\) liên tục trên \(R,\) có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right)=\left| f\left( \left| 6x-5 \right| \right)+2021+m \right|\) Có 3 điểm cực đại?







