I. Các dạng đồ thị

1. Đồ thị hàm số bậc ba
\(y=ax^3+bx^2+cx+d \ \ (a\neq 0)\)
\(y'=3ax^2+2bx+c\)
* a > 0

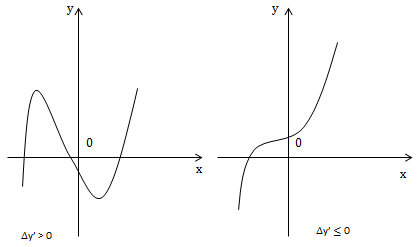
Đặc biệt:

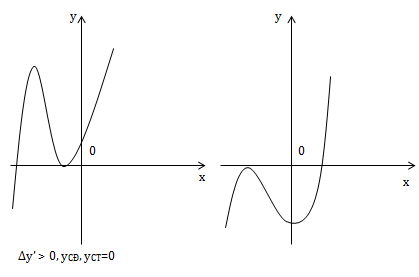
* a < 0


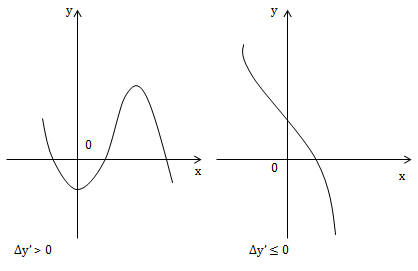
Đặc biệt

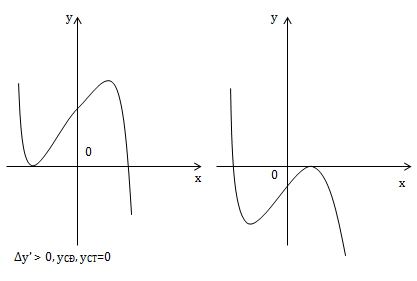
Nhận xét: 
1) Đồ thị hàm bậc ba\(y=ax^3+bx^2+cx+d \ \ (a\neq 0)\) cắt Ox tại 3 điểm phân biệt khi \(\left\{\begin{matrix} \Delta y'>0\\ y_{CD}.y_{CT}<0 \end{matrix}\right.\)
2) Đồ thị hàm số bậc ba cắt Ox tại 2 điểm phân biệt khi \(\left\{\begin{matrix} \Delta y'>0\\ y_{CD}.y_{CT}=0 \end{matrix}\right.\)
3) Đồ thị hàm số bậc ba cắt Ox tại 1 điểm duy nhất khi \(\bigg \lbrack\begin{matrix} \Delta y'\leq 0\\ \left\{\begin{matrix} \Delta y'>0 \\ y_{CD}.y_{CT}>0\\ \end{matrix}\right. \end{matrix}\)
2) Đồ thi hàm bậc bốn trùng phương
\(y=ax^4+bx^2+c \ \ (a\neq 0)\)
\(y'=4ax^3+2bx=2x(2ax^2+b)\)
* a > 0

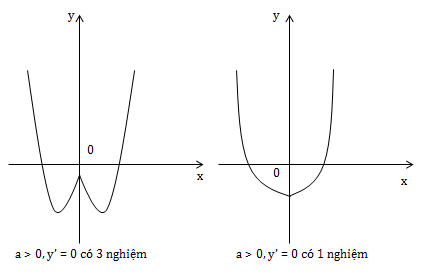
* a < 0 

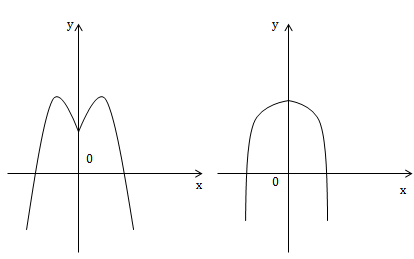
* Nhận xét:
1) Điều kiện để hàm số \(y=ax^4 +bx^2+c \ \ (a\neq 0)\) có 2 cực tiểu và 1 cực đại là \(\left\{\begin{matrix} a>0\\ y'=0 \end{matrix}\right.\) có 3 nghiệm phân biệt \((2ax^2+b=0\) có 2 nghiệm phân biệt)
2) Điều kiện để hàm số \(y=ax^4+bx^2+c \ \ (a\neq 0)\) có 2 cực đại và 1 cực tiểu là \(\left\{\begin{matrix} a<0\\ ab<0 \end{matrix}\right.\)
3) Điều kiện để hàm số \(y=ax^4+bx^2+c \ \ (a\neq 0)\) có đúng 1 cực trị \(\bigg \lbrack\begin{matrix} ab>0\\ b=0 \end{matrix}\)
4) Điều kiện để hàm số \(y=ax^4+bx^2+c \ \ (a\neq 0)\) có đúng 1 cực đại \(\left\{\begin{matrix} a<0\\ \bigg \lbrack\begin{matrix} ab>0\\ b=0 \end{matrix} \end{matrix}\right.\)
5) Điều kiện để hàm số \(y=ax^4+bx^2+c \ \ (a\neq 0)\) có đúng 1 cực tiểu \(\left\{\begin{matrix} a>0\\ \bigg \lbrack\begin{matrix} ab>0\\ b=0 \end{matrix} \end{matrix}\right.\)
3) Đồ thị hàm số \(y=\frac{ax+b}{cx+d}\)
\(y'=\frac{ad-bc}{(cx+d)^2}\)
+ ad - bc > 0: Hàm số đồng biến trên 2 khoảng \((-\infty ;-\frac{d}{c});(-\frac{d}{c};+\infty )\)
+ ad - bc < 0: Hàm số nghịch biến trên 2 khoảng \((-\infty ;-\frac{d}{c});(-\frac{d}{c};+\infty )\)

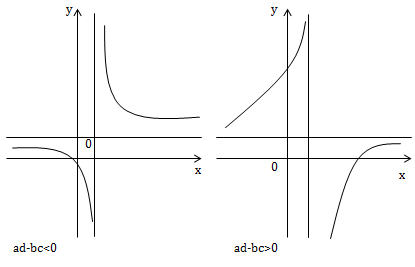
II. Một số phép biến đổi đồ thị
\((C): y=f(x)\)
1) Từ (C) suy ra \((C_1): y=f(\left | x \right |)\)
\(\left\{\begin{matrix} f(x) \ \ x\geq 0\\ f(-x) \ \ x < 0 \end{matrix}\right.\)
Đồ thị (C1):
+ Giữ nguyên phần đồ thị (C) ở bên phải trục tung.
+ Lấy đối xứng phần giữ nguyên qua Oy.

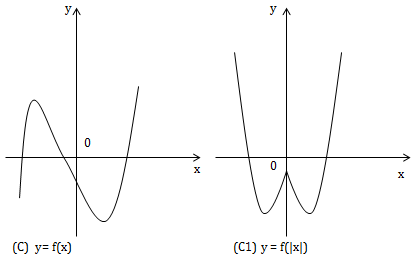
2) Từ (C) suy ra \((C_2): y=(f\left | x \right |)\)
\(\left\{\begin{matrix} f(x) \ neu \ f(x) \geq 0\\ -f(x) \ neu \ f(x) <0 \end{matrix}\right.\)
Đồ thị (C₂):
+ Giữ nguyên phần đồ thị (C) ở giá trên Ox
+ Lấy đối xứng phần đồ thị (C) ở dưới Ox qua Ox.

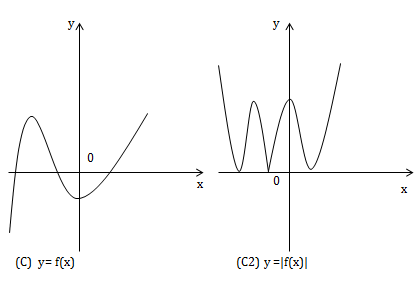
3) Từ (C) suy ra \(y=|f(x)|\)

\(y=|f(x)|=\left\{\begin{matrix} f(x) \ f(|x|)\geq 0\\ -f(x) \ f(|x|)< 0 \end{matrix}\right.\)
bằng cách 
+ giữ nguyên phần đồ thị (C1) ở phía trên Ox
+ Lấy đối xứng phần đồ thị (C1) ở phía dưới Ox qua Ox.

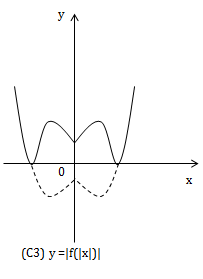
4) Từ (C) suy ra (C4) |y| = f(x)
\(\left\{\begin{matrix} f(x)\geq 0\\ \bigg \lbrack\begin{matrix} y=f(x)\\ y=-f(x) \end{matrix} \end{matrix}\right.\)
(C₄) gồm 
+ Phần đồ thị (C) ở phía trên Ox
+ Lấy đối xứng phần đồ thị (C) ở phía trên Ox qua Ox

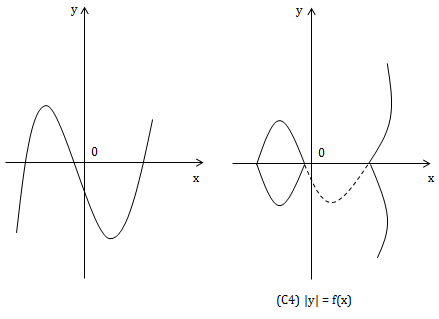
5) Từ (C) suy ra (C5) y = f(x+a)
Tịnh tiến (C) theo vecto \(\vec{u}=(-a;0)\)

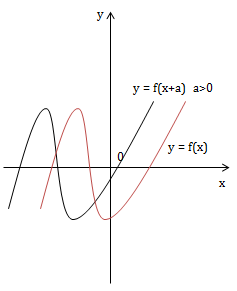
6) Từ (C) suy ra (C6) y = f(x)+b
Tịnh tiến (C) theo \(\vec{v}=(0;b)\)
III. Bài tập

Ví dụ 1: Tìm m để đường thẳng y = m cắt đồ thị \(y=-x^3+3x-1\) tại 3 điểm phân biệt. 

Giải
Cách 1: 
TXĐ: R
\(y'=-3x^2+3, y'=0\Leftrightarrow x=\pm 1\)


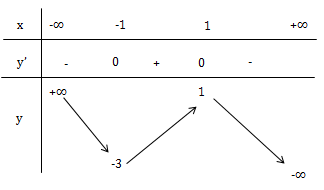
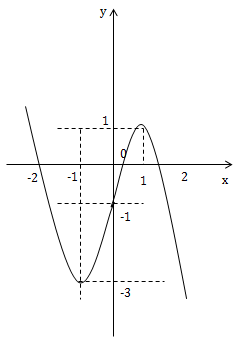
. Đường thẳng y = m, vuông góc oy cắt trục tại A(0;m)
. Để y = m cắt đồ thị tại 3 điểm phân biệt thì \(-3 Cách 2:

Số giao điểm đường thẳng y =m và đồ thị \(y=-x^3+3x-1\) là số nghiệm phương trình \(-x^3+3x-1=m\Leftrightarrow x^3-3x+1+m=0\) là số giao điểm y = 0 với đồ thị \(y=x^3-3x+1+m\)
Xét \(f(x)=x^3-3x+1+m\)
\(f'(x)=3x^2-3, f'(x)=0\Leftrightarrow x=\pm 1\)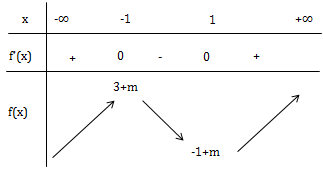
\(y_{cbt}\Leftrightarrow \left\{\begin{matrix} \Delta y'>0\\ y_{CD}.y_{CT}<0 \end{matrix}\right.\Leftrightarrow (3+m).(-1+m)<0\Leftrightarrow -3 Câu 1: Tập hợp m để đường thẳng y = m cắt đồ thị \(y=-x^3+3x-1\) tại 3 điểm phân biệt là 
A. (-3;1)
Câu 2: Tập hợp m để đường thẳng y = m cắt đồ thị \(y=-x^3+3x-1\) tại 2 điểm phân biệt là 
A. {-3; 1}    B. (-3; 1)   
Câu 3: Tập hợp m để đường thẳng y = m cắt đồ thị \(y=-x^3+3x-1\) tại 1 điểm phân biệt là 
A. \((-\infty ;-3);(1;+\infty )\)
Câu 4: Tập hợp m để đồ thị \(y=x^3-3x+1+m\) cắt Ox tại 3 điểm phân biệt
A. (-3; 1)
Câu 5: Tập hợp m để đồ thị \(y=x^3-3x+1+m\) cắt Ox tại 2 điểm phân biệt
A. {-3; 1}   B. (-3; 1)
VD2: Tìm m để đường thẳng y = m + 3 cắt đồ thị hàm số \(y=x^4-2x\) tại 3 điểm phân biệt.
Giải
\(y'=4x^3-4x, y'=0\Leftrightarrow 4x(x^2-1)=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x =0\\ x=\pm 1 \end{matrix}\)

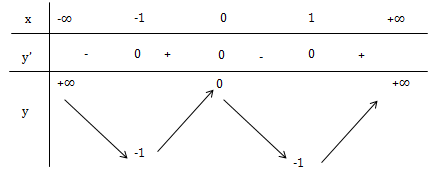
\(y_{cbt}\Leftrightarrow m+3=0\Leftrightarrow m=-3\)
Câu 1: Tập hợp m để y = m + 3 cắt đồ thị \(y=x^4-2x^2\) tại 3 điểm phân biệt là.
A. {-3}
Câu 2: Tập hợp m để y = m + 3 cắt đồ thị \(y=x^4-2x^2\) tại 4 điểm phân biệt là.
A.(-4; -3)
Câu 3: Tập hợp m để y = m + 3 cắt đồ thị \(y=x^4-2x^2\) tại 2 điểm phân biệt là.
A. \(\left \{ -4 \right \}\cup (-3;+\infty )\)
Câu 4: Tập hợp m để y = m + 3 cắt đồ thị \(y=x^4-2x^2\) 
A.\((-\infty ;-4)\)
Câu 5: Tìm m để y = 3 cắt đồ thị \(y=x^4-2x^2-m\) tại 4 điểm phân biệt là.
A.(-4; -3)
VD3: Tìm m để đường thẳng y = m cắt đồ thị \(y=\frac{x-2}{x+1}\) tại 1 điểm duy nhất có hoành độ dương.
Giải
Xét hàm số \(y=\frac{x-2}{x+1}\)
TXĐ: D = R \ {-1}
\(y'=\frac{3}{(x+1)^2}\)

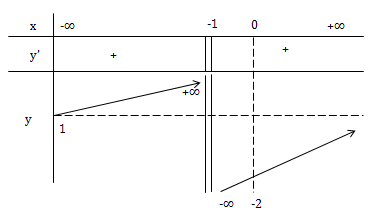
Từ bảng biến thiên ta có: \(y_{cbt}\Leftrightarrow -2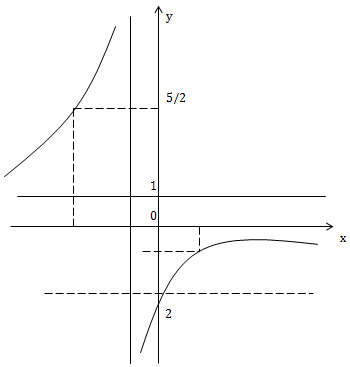
Câu 1: Tập hợp m để đường thẳng y = m cắt đồ thị tại điểm có hoành độ dương
A. (-2;1)
Câu 2: Tập hợp m để đường thẳng y = m cắt đồ thị điểm có hoành độ âm.
A. \((1;+\infty );(-\infty ;-2)\)
Câu 3: Cho (C) \(y=\frac{x-2}{x+1}\)
Trong các đồ thị sau đồ thị nào là đồ thị \(y=\left | \frac{x-2}{x+1} \right | \ \ (C_1)\)
Câu 4: Cho (C) \(y=\frac{x-2}{x+1}\)

Trong các đồ thị sau đồ thị nào là đồ 
\(y=\frac{\left |x \right |-2}{\left |x \right |+1}\)