Trong bài học hôm nay chúng ta sẽ xét ứng dụng của tính đơn điệu để giải hệ phương trình và hệ bất phương trình, trong việc mà chúng ta muốn giải hệ hoặc là bất phương trình thì chúng cần xác định được chúng ta xét hàm nào, xét trên miền nào. Và các kỹ thuật chúng ta xác định hàm và miền thì nó cũng giống như trong bài toán giải phương trình và bất phương trình.

VD1: Giải hệ phương trình \(\left\{\begin{matrix} cotx-coty=x-y\\ 3x+5y=2\pi\\ 0

Giải
\(\left\{\begin{matrix} 3x+5y=2\pi\\ 0 Xét \(f(t)=cott-t\) trên \((0;\frac{2\pi}{3})\)​
\(f'(t)=-\frac{1}{sin^2t}-1<0\)
f(t) nghịch biến trên \((0;\frac{2\pi}{3})\)
\((1)\Leftrightarrow cotx-x=coty-y\)
\(\Leftrightarrow f(x)=f(y)\)
lại có f(t) nghịch biến trên \((0;\frac{2\pi}{3}), x,y\in (0;\frac{2\pi}{3})\)
suy ra x = y
Hệ pt \(\Leftrightarrow \left\{\begin{matrix} x=y\\ 3x+5y=2\pi\\ 0 VD2: Giải hệ phương trình \(\left\{\begin{matrix} x-\frac{1}{x}=y-\frac{1}{y}\\ 2y=x^3+1 \end{matrix}\right.\) (A-2003)
Giải
ĐK: \(x,y\neq 0\)
Xét \(f(t)=t-\frac{1}{t}\)  nên \((-\infty ;0);(0;+\infty )\)
\(f'(t)=1+\frac{1}{t^2}>0\)
f(t) đồng biến trên 2 khoảng \((-\infty ;0);(0;+\infty )\)
TH1: \(x,y\in (0;+\infty )\)
\((1)\Leftrightarrow f(x)=f(y)\)
lại có f(t) đồng biến trên \((0;+\infty )\)
Suy ra x = y
Hệ pt  \(\Leftrightarrow \left\{\begin{matrix} x=y>0\\ 2y=x^3+1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=y>0\\ x^3-2x+1=0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=y>0\\ (x-1)(x^3+x-1)=0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x=1\\ \bigg \lbrack\begin{matrix} x=\frac{-1-\sqrt{5}}{2} \ (loai)\\ x=\frac{-1+\sqrt{5}}{2} \ \ \ \ \ \ \end{matrix} \end{matrix}\right.\)
Vậy \(\left\{\begin{matrix} x=y=1\\ x=y=\frac{1+\sqrt{5}}{2} \end{matrix}\right.\)
TH2: \(x,y\in (-\infty ;0)\)
Tương tự hệ \(\left\{\begin{matrix} x=y<0\\ 2y=x^3+1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=y<0\\ x^3-2x+1=0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=y<0 \ (loai)\\ \Bigg \lbrack\begin{matrix} x=1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x=\frac{-1-\sqrt{5}}{2}\ \ \ \ \ \ \ \ \ \ \ \\ x=\frac{-1+\sqrt{5}}{2} \ (loai) \end{matrix} \end{matrix}\right.\)
\(\Leftrightarrow x=y=\frac{-1-\sqrt{5}}{2}\)
TH3: \(\left\{\begin{matrix} x>0\\ y<0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x^3+1>0\\ 2y<0 \end{matrix}\right.\)
\(\Rightarrow 2y \(\left\{\begin{matrix} x<0\\ y>0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x^3+1<1\\ 2y>0 \end{matrix}\right. \Rightarrow \left\{\begin{matrix} 2y<1\\ x^3+1>0 \end{matrix}\right.\)
TH4: \(\left\{\begin{matrix} 0 f(t) đồng biến trên \((-\infty ;0)(0;+\infty )\)
\(-1 \(0 Không thỏa mãn pt \(x-\frac{1}{x}=y-\frac{1}{y}\)
KL: Nghiệm hệ pt là  \(\left\{\begin{matrix} x=1\\ y=1 \end{matrix}\right., \left\{\begin{matrix} x=\frac{-1+\sqrt{5}}{2}\\ y=\frac{-1+\sqrt{5}}{2} \end{matrix}\right.,\left\{\begin{matrix} x=\frac{-1-\sqrt{5}}{2}\\ y=\frac{-1-\sqrt{5}}{2} \end{matrix}\right.\)
VD3: Giải hệ phương trình \(\left\{\begin{matrix} 2x+1=y^3+y^2+y\\ 2y+1=z^3+z^2+z\\ 2z+1=x^3+x^2+x \end{matrix}\right.\)
Giải
\(\left\{\begin{matrix} x=\frac{1}{2}(y^3+y^2+y-1)\\ y=\frac{1}{2}(z^3+z^2+z-1)\\ z=\frac{1}{2}(x^3+x^2+x-1) \end{matrix}\right.\)
Xét \(f(t)=\frac{1}{2}(t^3+t^2+t-1)\)
Từ hệ ta có \(\left\{\begin{matrix} x=f(y)\\ y=f(z)\\ z=f(x) \end{matrix}\right.\Rightarrow x=f(f(f(x)))\)
\(f'(t)=\frac{1}{2}(3t^2+2t+1)>0\)
Vì a =3 > 0
\(\Delta '=1-3<0\)
f(t) đồng biến trên R
\(x>f(x)\Leftrightarrow f(x)>f(f(x))\Rightarrow f(f(x))>f(f(f(x)))\)
Suy ra x > x ( vô lý)
x< f(x) tương tự x < x (vô lý)
x = f(x) thỏa mãn hệ
\(\Leftrightarrow x=\frac{1}{2}(x^3+x^2+x-1)\)
\(\Leftrightarrow x^3+x^2+x-1=2x\)
\(\Leftrightarrow x^3+x^2-x-1=0\)
\(\Leftrightarrow x^2(x+1)-(x+1)=0\)
\(\Leftrightarrow (x^2-1)(x+1)=0\)
\(\Leftrightarrow (x+1)^2(x-1)=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x=1\\ x=-1 \end{matrix}\)
Từ hệ phương trình 
x=y=z=1
x=y=z=-1
VD4: Giải phương trình \(\left\{\begin{matrix} 3x^2+2x-1<0\\ x^3-3x+1>0 \end{matrix}\right.\)
Giải
\((1)\Leftrightarrow -1 Xét \(f(x)=x^3-3x+1\) nên \((-1;\frac{1}{3})\)
\(f'(x)=3x^2-3, f'(x)=0\Leftrightarrow x^2-1=0\)
\(\Leftrightarrow \Bigg \lbrack \begin{matrix} x=1\notin (-1;\frac{1}{3})\\ \\ x=-1 \notin (-1;\frac{1}{3}) \end{matrix}\)

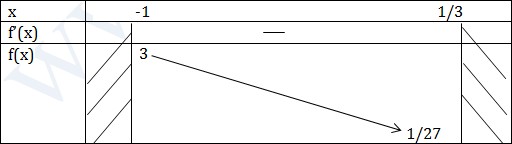
Từ bảng biến thiên \(f(x)>0\forall x\in (-1;\frac{1}{3})\)

Tập nghiệm hệ bất phương trình \((-1;\frac{1}{3})\)