Hôm trước chúng ta đã học xong phần lý thuyết của phần ADN, gen, mã di truyền. Và hôm nay chúng ta sẽ ôn tập lại các ý chính và học một số công thức, phương pháp giúp các em biết cách giải các bài tập của phần này.

1. Công thức và bài tập ADN, gen
Gọi N số nu của gen (ADN)
+ \(\sum N = A+T+G+X = 2A + 2G \ (A=T \ \&\ G=X)\)
+ Chiều dài gen (ADN)
\(l=\frac{N}{2}.3,4.A^0\) (1 nu có chiều dài 3,4A⁰)
\(1m\rightarrow 10^3mm\rightarrow 10^6\mu \rightarrow 10^9nm\rightarrow 10^{10}A^0\)
+ Chu kỳ xoắn
\(C = \frac{N}{20}\) (1 chu kỳ xoắn = 10 cặp nu = 20 nu)
+ Khối lượng gen (ADN)
M = N.300 (1 nu có khối lượng 300 đvC)
+ Số liên kết H₂
H = 2A + 3G
+ Số liên kết hóa trị

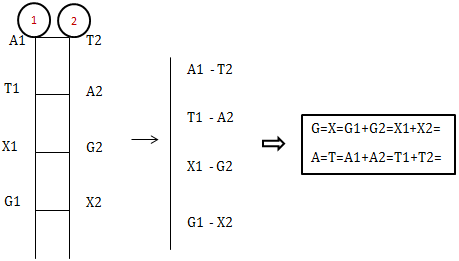
- Số liên kết hóa trị giữa các nu
⇒ Số liên kế HT trên 1 mạch \(\frac{N}{2}-1\)
⇒ Sô liên kết H₂ giữa các nu trong gen (ADN) \(2\left ( \frac{N}{2}-1 \right ) = N - 2\)
- Số liên kết hóa trị trong toàn bộ gen (ADN)
+ Số liên kết hóa trị giữa các nu N-2 (liên kết)
+ Số liên kết hóa trị trong các nu N (liên kết)
⇒ ∑ LKHT trong ADN = 2N - 2
+ Công thức mối liên hệ các u trên 2 mạch đơn

2. Dạng bài tập mã di truyền
- Số mã di truyền ​\(\frac{N}{2.3}=\frac{r.N}{3}\)
- Số  bộ ba mã hóa: \(\frac{N}{2.3}-1\) (trừ mã kết thúc)
- Số kiểu bộ 3
Gọi a là số nu tham gia vào cấu trúc gen hay ADN
⇒ Số kiểu bộ 3: a3

* Các ví dụ
VD1: Một gen có chiều dài 510nm. Hiệu số giữa A với mọt loại nu khác nhau bằng 10% tổng số nu của gen. Trên mạch đơn thứ nhất của gen có 300A và 250G.
a. Tính số lượng và tỉ lệ % từng loại nu trên mỗi mạch đơn gen?
b. Tính số liên kết H₂, số liên kết hóa trị và số chu kỳ xoắn gen?
Giải
a.
L = 510 nm = 5100 A⁰
Ta có \(\left\{\begin{matrix} \%A-\%G=10\%\\ \%A+\%G=50\% \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} A=T=30\%\\ G=X=20\% \end{matrix}\right.\)
\(A_1=300=T_2\)
\(G_1=200=X_2\)
N = 3000 (nu)
\(\Rightarrow \left\{\begin{matrix} A=T=300 \% =900\\ G=X=20\%=600 \end{matrix}\right.\)
⇒ A₂ = A - A₁ = 600 = T₁
A₁ = 300 = T₂
G₂ = G - G₁ = 350 = X₁ = 23,37%
G₁ = X₂ = 250 - 16,67%
A₁ = T₂ = 20%
T₁ = A₂ = 40%
X₁ = G₂ = 23,37%
G₁ = X₂ = 16,67%
b)
Số liên kết H₂ = 2A + 3G = 3600
Số liên kết hóa trị = 2N + 2 = 5998
Số chu kỳ xoắn H₂ = 2A + 3G = 3600

VD2: Một gen được cấu tạo từ 4 loại từ 4 loại nu A, T, G, X và 4 loại nu này tạo ra 64 bộ ba. Hãy xác định:
a. Có bao nhiêu bộ ba không chứa A.
b. Có bao nhiêu bộ ba chứa ít nhất 1 nu loại A.
Giải
ADN cấu tạo cấu tạo từ 4 loại nu
A, T, G, X ⇒ 64 bộ ba
a) Ta có a = 3 ⇒ Số bộ ba không chứa
A = 3³ = 27
b) Chứa ít nhất 1A = chứa 1A
                               chứa 2A
                               chứa 3A
= 64 - 27 = 37