Hôm nay chúng ta học tiếp bài số 3 Con lắc đơn. Vậy con lắc đơn là gì?

Thực ra bài con lắc đơn các em đã được học ở chương trình lớp 10. Nhưng hôm nay chúng ta sẽ tìm hiểu sâu hơn cũng như ôn tập lại các kiến thức trọng tâm về con lắc đơn để chuẩn bị cho kỳ thi THPT sắp tới.

I. Cấu tạo
Gồm 1 sợi dây mềm, nhẹ, không co giãn và một quả cầu khối lượng m.

II. Phương trình động lực học của con lắc đơn

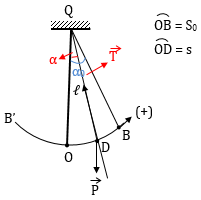
Theo định luật II Niuton
\(\overrightarrow{T} + \overrightarrow{P} = m\overrightarrow{a} (*)\)
Chiếu (*) lên phương trình tiếp tuyến:
\(P_t = ma_t\)
Với \(\left\{\begin{matrix} P_t = -P\sin \alpha = - mg \sin \alpha \\ a_t = s'' \hspace{3,5cm} \end{matrix}\right.\)
\(\Rightarrow -g \sin \alpha = s'' \ (1)\)
* Nếu \(\mathbf{\alpha _0 \leq 10^0}\)
\(\Rightarrow \sin \alpha \approx \alpha = \frac{s}{\ell}\)
\(\Rightarrow -g.\frac{s}{\ell} = s'' \Leftrightarrow s'' = -\frac{g}{\ell}.s\)
Đặt \(\omega ^2 = \frac{g}{\ell} \Rightarrow s'' = -\omega ^2.s \ (2)\)
Nghiệm của (2) có dạng
\(s = S_0.\cos (\omega t + \varphi )\)
Vậy dao động bé \((\alpha _0 \leq 10^0)\) của con lắc đơn là dao động điều hòa với chu kỳ \(T = \frac{2 \pi}{\omega } = 2 \pi \sqrt{\frac{\ell}{g}}\)
* Các phương trình của con lắc đơn dao động điều hòa
+ Phương trình li độ:
Dài: \(s = S_0 \cos (\omega t + \varphi )\)
Góc: \(\alpha = \alpha _0 \cos (\omega t + \varphi )\)
\((S_0 = \alpha _0.\ell;\ s = \alpha .\ell)\)
+ Phương trình vận tốc: \(v = s' = -\omega S_0.\sin (\omega t + \varphi )\)
+ Phương trình gia tốc: \(a = v' = s''\)
\(\Rightarrow a = -\omega ^2.S_0. \cos (\omega t + \varphi ) = -\omega ^2s\)
* Năng lượng con lắc đơn dao động điều hòa
• W_đ \(=\frac{1}{2}mv^2 = \frac{1}{2}m\omega ^2S_{0}^{2}. \sin^2 (\omega t + \varphi )\)
• W_t \(=\frac{1}{2}m\omega ^2 s^2= \frac{1}{2}m\omega ^2S_{0}^{2}. \cos ^2 (\omega t + \varphi )\)
• W = W_đ + W_t = \(\frac{1}{2}mv^2 + \frac{1}{2}m \omega ^2 s^2\) = hằng số
Nhận xét: Đối với con lắc đơn dao động điều hòa thì bài tập tương tự con lắc lò xo nếu thay \(s = x; S_0 = A; m\omega ^2 = k\)
* Xét năng lượng - vận tốc - lực căng dây trong trường hợp tổng quát
+ Năng lượng:
• W_đ \(=\frac{1}{2}mv^2\)
• \(W_t = ph = mg\ell (1-\cos \alpha )\)
⇒ W = W_đ + W_t = \(\frac{1}{2}mv^2 + mg \ell (1 - \cos \alpha )\) (hằng số)
W = W_{đ max} = \(\frac{1}{2}mv_{max}^{2}\) (VTCB)
\(W = W_{t \ max} = mg\ell (1 - \cos \alpha _0)\)
 + Vận tốc:
Ta có: W_đ + W_t = W_t max
\(\Rightarrow \frac{1}{2}mv^2 + mg\ell (1-\cos \alpha ) = mg \ell (1-\cos \alpha _0)\)
\(\Rightarrow v^2 = 2g\ell (\cos \alpha - \cos \alpha _0)\)
• \(|v|_{max} = \sqrt{2g \ell (1-\cos \alpha _0)}\) (VTCB)
• \(|v|_{min} = 0\) (VT biên)
+ Lực căng dây:
Chiếu (*) lên phương sợi dây, chiều dương hướng tâm: T - P_n = ma_ht
Với \(\left\{\begin{matrix} P_n = P.\cos = mg \cos \alpha \hspace{1,2cm}\\ a_{ht} = \frac{v^2}{\ell } = 2g(\cos \alpha - \cos \alpha _0) \end{matrix}\right.\)
\(\Rightarrow T = mg\cos \alpha + m.2g(\cos \alpha - \cos \alpha _0)\)
\(\Rightarrow T = mg(3 \cos \alpha - 2\cos \alpha _0)\)
\(\cdot \ T_{max} = mg(3 - 2 \cos \alpha _0) > P\)
\(\cdot \ T_{min} = mg\cos \alpha _0 < P\)