Mời các em cùng theo dõi bài giảng Bài 9: Chuyển động thẳng biến đổi đều môn Vật Lý 10 chương trình Kết nối tri thức do HOC247 biên soạn để nắm được các kiến thức cơ bản về: đồ thị độ dịch chuyển – thời gian của chuyển động thẳng, vận tốc, hệ số góc (độ dốc) của đường biểu diễn trong đồ thị...Nội dung cụ thể chi tiết mời các em cùng tham khảo dưới đây.
Tóm tắt lý thuyết
1.1. Gia tốc của chuyển động thẳng biến đổi đều
- Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.
- Chuyển động thẳng có độ lớn vận tốc tăng đều theo thời gian gọi là chuyển động thẳng nhanh dần đều; chuyển động thẳng có độ lớn vận tốc giảm đều theo thời gian gọi là chuyển động thẳng chậm dần đều.
- Vì chuyển động thẳng biến đổi đều có vận tốc thay đổi đều theo thời gian nên gia tốc không đổi theo thời gian: \(a=\dfrac{\Delta\text{v}}{\Delta t}=\) hằng số
|
- Chuyển động thẳng nhanh dần đều là chuyển động thẳng có độ lớn vận tốc tăng đều theo thời gian. - Chuyển động thẳng chậm dần đều là chuyển động thẳng có độ lớn vận tốc giảm đều theo thời gian. |
|---|
1.2. Vận tốc tức thời của chuyển động thẳng biến đổi đều
Gọi \(\text{v}_0\) là vận tốc tại thời điểm ban đầu \(t_0\), \(\text{v}_t\) là vận tốc tại thời điểm \(t\).
Vì \(a=\dfrac{\Delta\text{v}}{\Delta t}=\dfrac{\text{v}_t-\text{v}_0}{t-t_0}=\dfrac{\text{v}_t-\text{v}_0}{\Delta t}\) nên \(\text{v}_t=\text{v}_0+a.\Delta t\)
Nếu ở thời điểm ban đầu \(t_0=0\) thì: \(\text{v}_t=\text{v}_0+a.t\)
Nếu ở thời điểm ban đầu \(t_0=0\) vật mới bắt đầu chuyển động thì: \(\text{v}_0=0\) và \(\text{v}_t=a.t\)
1.3. Đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều
Vận tốc tức thời v trong chuyển động thẳng biến đổi đều là hàm bậc nhất của thời gian t, nên đồ thị vận tốc – thời gian của chuyển động này có các dạng như sau:
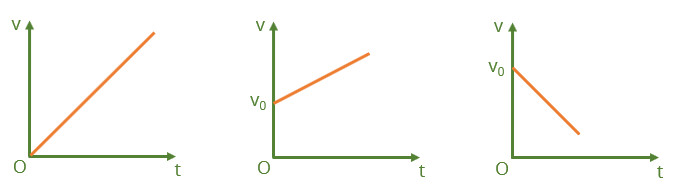
Các dạng đồ thị vận tốc - thời gian trong chuyển động thẳng biến đổi đều
1.4. Độ dịch chuyển của chuyển động thẳng biến đổi đều
a. Tính độ dịch chuyển bằng đồ thị vận tốc – thời gian (v - t)
- Trong khoảng thời gian t, nếu vật chuyển động thẳng đều với vận tốc v, thì đồ thị (v – t) có dạng như hình dưới đây và độ dịch chuyển trong thời gian này có độ lớn là: \(d=\text{v}.t\).

Độ lớn này bằng diện tích của của hình chữ nhật, các cạnh có độ dài là v và t. Diện tích này gọi là diện tích giới hạn của đồ thị (v – t) đối với trục hoành.
- Trong thời gian t, nếu vật chuyển động thẳng biến đổi đều với vận tốc ban đầu v0 thì công thức tính vận tốc là \(\text{v}_t=\text{v}_0+a.t\), đồ thị (v – t) có dạng như hình dưới đây.
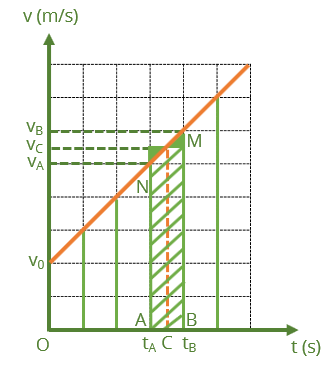
Có thể dựa vào đồ thị này để tính độ dịch chuyển.
Kẻ các đường song song với trục tung Ov, cách nhau một khoảng ∆t rất nhỏ để chia đồ thị thành các hình thang nhỏ có đường cao ∆t.
Chọn một hình thang nhỏ bất kì trong hình. Vì vật chuyển động thẳng biến đổi đều nên trong khoảng thời gian nhỏ từ tA đến tB, có thể coi chuyển động của vật là thẳng đều với vận tốc \(\text{v}_C=\dfrac{\text{v}_A+\text{v}_B}{2}\) (C nằm giữa A và B).
Độ dịch chuyển của vật trong thời gian ∆t có độ lớn bằng diện tích hình chữ nhật có cạnh là vC và ∆t. Hình vẽ cho thấy diện tích của hình này bằng điện thích của hình thang nhỏ gạch chéo có đường cao ∆t và các đáy có độ dài vA, vB.
Độ dịch chuyển trong thời gian t, bằng tổng các độ dịch chuyển trong các khoảng thời gian ∆t, nên có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
b. Tính độ dịch chuyển bằng công thức
Bài toán: Biết độ dịch chuyển trong chuyển động thẳng biến đổi đều có độ lớn bằng diện tích giới hạn đồ thị (v – t) trong thời gian t của chuyển động. Hãy chứng minh rằng công thức tính độ lớn của độ dịch chuyển trong chuyển động thẳng biến đổi đều là: \(d = {v_0}t + \frac{1}{2}a{t^2}\)
Chứng minh rằng: \({v^2} - v_0^2 = 2.a.d\)
Bài giải
- Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
- Diện tích hình thang: \(d = {s_{ht}} = \frac{{(v + {v_0}).t}}{2} = \frac{1}{2}{v_0}t + \frac{1}{2}vt\) (1)
- Lại có: \(a = \frac{{v - {v_0}}}{t} \Rightarrow v = at + {v_0}\) (2)
- Thay (2) vào (1) ta được:
\(d = \frac{1}{2}{v_0}t + \frac{1}{2}(at + {v_0})t = \frac{1}{2}{v_0}t + \frac{1}{2}a{t^2} + \frac{1}{2}{v_0}t\)
\( \Rightarrow d = {v_0}t + \frac{1}{2}a{t^2}\) (đpcm)
Mặt khác \({v_t} = {v_0} + at\) (*)
\(d = {v_0}t + \frac{1}{2}a{t^2}\) (**)
+ Bình phương 2 vế của (*) ta được:
\({v^2} = v_0^2 + 2{v_0}.at + {a^2}{t^2} = v_0^2 + a(2{v_0}t + a{t^2})\) (1)
+ Từ (**) ta có:
\(2{\rm{d}} = 2{v_0}t + a{t^2}\) (2)
Thay (2) vào (1) ta được:
\({v^2} = v_0^2 + a.2{\rm{d}} \Leftrightarrow {v^2} - v_0^2 = 2{\rm{a}}.d\) (đpcm)
|
Hệ số góc của đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều cho biết giá trị của gia tốc. Các công thức của chuyển động thẳng biến đổi đều: \(\text{v}_t=\text{v}_0+a.t\) \(d=\text{v}_0.t+\dfrac{1}{2}.a.t^2\) \(\text{v}_t^2-\text{v}_0^2=2.a.d\) |
|---|
Bài tập minh họa
Bài 1: Hãy tính độ dịch chuyển của chuyển động có đồ thị (v-t) ở hình vẽ dưới đây.
.png)
Biết mỗi cạnh của ô vuông nhỏ trên trục tương ứng với 2 m/s, trên trục hoành ứng với 1s.
Hướng dẫn giải
Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{v_0} = 4\left( {m/s} \right);v = 16\left( {m/s} \right)\\t = 6\left( s \right)\end{array} \right.\)
Suy ra: Độ dịch chuyển là:
\(d = \frac{{\left( {4 + 16} \right).6}}{2} = 60\left( m \right)\)
Bài 2: Hãy dùng đồ thị (v – t) sau đây để:
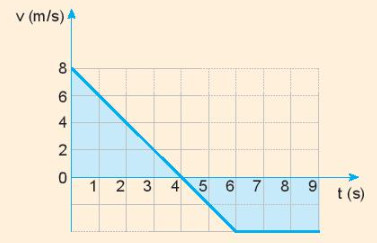
a) Mô tả chuyển động
b) Tính độ dịch chuyển trong 4 giây đầu, 2 giây tiếp theo và 3 giây cuối
c) Tính gia tốc của chuyển động trong 4 giây đầu
d) Tính gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6.
Kiểm tra kết quả của câu b và câu c bằng cách dùng công thức.
Hướng dẫn giải
a) Mô tả chuyển động:
- Trong 4 giây đầu tiên: chuyển động chậm dần đều từ 8 m/s đến 0 m/s
- Từ giây thứ 4 đến giây thứ 6: bắt đầu tăng tốc với vận tốc -2 m/s
- Từ giây thứ 6 đến giây thứ 9: chuyển động thẳng đều với vận tốc – 2 m/s
b) Độ dịch chuyển:
- Trong 4 giây đầu:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_1} = \frac{1}{2}.{t_1}.{v_1} = \frac{1}{2}.4.8 = 16\left( m \right)\)
- Trong 2 giây tiếp theo:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_2} = \frac{1}{2}.{t_2}.{v_2} = \frac{1}{2}.2.( - 4) = - 4\left( m \right)\)
- Trong 3 giây cuối:
Độ dịch cuyển bằng diện tích hình chữ nhật có chiều dài là t và chiều rộng là v.
\({d_3} = {v_3}.{t_3} = - 4.3 = - 12\left( m \right)\)
c)
Gia tốc của chuyển động trong 4 giây đầu:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{8 - 0}}{{4 - 0}} = 2\left( {m/{s^2}} \right)\)
d)
Gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 4 - 0}}{{6 - 4}} = - 2\left( {m/{s^2}} \right)\)
* Kiểm tra kết quả bằng công thức:
Độ dịch chuyển:
- Trong 4 giây đầu:
\({d_1} = {v_0}{t_1} + \frac{1}{2}a{t_1}^2 = 0.4 + \frac{1}{2}{.2.4^2} = 16\left( m \right)\)
- Trong 2 giây tiếp theo:
\({d_2} = {v_0}{t_2} + \frac{1}{2}a{t_2}^2 = 0.2 + \frac{1}{2}.( - 2){.2^2} = - 4\left( m \right)\)
- Trong 3 giây cuối:
\({d_3} = {v_3}t = - 4.3 = - 12\left( m \right)\)
→ Trùng với kết quả khi dùng đồ thị.
Luyện tập Bài 9 Vật Lý 10 KNTT
Sau bài học này, học sinh có thể:
- Vẽ được đồ thị độ dịch chuyển – thời gian của chuyển động thẳng.
- Dựa vào đồ thị độ dịch chuyển - thời gian, xác định được vị trí và vận tốc của vật ở bất kì thời điểm nào.
3.1. Trắc nghiệm Bài 9 môn Vật Lý 10 KNTT
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật Lý 10 KNTT Bài 9 cực hay có đáp án và lời giải chi tiết.
-
- A. 1 h
- B. 0,5 h
- C. 2 h
- D. 3 h
-
- A. 2m/s2
- B. 0,2m/s2
- C. 4m/s2
- D. 0,4m/s2
-
- A. \( \frac{3t}{2}\)
- B. \( \frac{t}{2}\)
- C. \( \frac{t}{4}\)
- D. \( \frac{3t}{4}\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 9 môn Vật Lý 10 KNTT
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật Lý 10 KNTT Bài 9 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Giải câu hỏi trang 40 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 1 trang 41 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 2 trang 41 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 1 trang 42 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 2 trang 42 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 3 trang 41 SGK Vật Lý 10 Kết nối tri thức - KNTT
Vận dụng 1 trang 43 SGK Vật Lý 10 Kết nối tri thức - KNTT
Vận dụng 2 trang 43 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.1 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.2 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.3 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.4 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.5 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.6 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.7 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.8 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.9 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.10 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.11 trang 17 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.12 trang 17 SBT Vật lý 10 Kết nối tri thức - KNTT
Hỏi đáp Bài 9 môn Vật Lý 10 KNTT
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 10 HỌC247







