Giải Bài tập 9.6 trang 16 SBT Vật lý 10 Kết nối tri thức
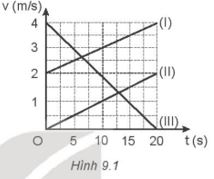
Hình 9.1 là đồ thị vận tốc - thời gian của ba chuyển động thẳng biến đổi đều.
a) Viết công thức tính vận tốc và độ dịch chuyển của mỗi chuyển động.
b) Tính độ dịch chuyển của chuyển động (III).
Hướng dẫn giải chi tiết Bài tập 9.6
Phương pháp giải:
- Sử dụng cách đọc số liệu từ đồ thị: xác định v0 và v tại một thời điểm t bất kì.
- Tính gia tốc của chuyển động: a = \(\frac{{\Delta v}}{{\Delta t}}\).
- Sử dụng công thức tính vận tốc và độ dịch chuyển của chuyển động thẳng biến đổi đều: \(v = {v_0} + at\); \(d = {v_0}t + \frac{1}{2}a{t^2}\).
Trong đó:
+ v0 là vận tốc tại thời điểm ban đầu.
+ v là vận tốc tại thời điểm t.
+ a là gia tốc của chuyển động.
+ d là độ dịch chuyển của chuyển động sau khoảng thời gian t.
Lời giải chi tiết:
a) Căn cứ vào đồ thị Hình 9.1 ta có thể xác định được:
- Chuyển động (I) có:
Vận tốc ban đầu: v01 = 2 m/s.
Vận tốc tại t = 20 s là v = 4 m/s.
Gia tốc của chuyển động là: a1 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{01}}}}{{\Delta t}}\)=\(\frac{{4 - 2}}{{20}}\)= 0,1 m/s2
Vận tốc của chuyển động là: \({v_1} = {v_{01}} + {a_1}t\)\( = \)\(2{\rm{ }} + {\rm{ }}0,1t\)(m/s).
Độ dịch chuyển của chuyển động: \({d_1} = {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)\( = 2t + 0,05{t^2}\)(m).
Tương tự, ta có:
- Chuyển động (II) có:
Vận tốc ban đầu: v02 = 0 m/s.
Vận tốc tại t = 20 s là v = 2 m/s.
Gia tốc của chuyển động là: a2 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{02}}}}{{\Delta t}}\)=\(\frac{{2 - 0}}{{20}}\)= 0,1 m/s2
Vận tốc của chuyển động là: \({v_2} = {v_{02}} + {a_2}t\)\( = \)\(0,1t\)(m/s).
Độ dịch chuyển của chuyển động: \({d_2} = {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)\( = 0,05{t^2}\)(m).
- Chuyển động (III) có:
Vận tốc ban đầu: v03 = 4 m/s.
Vận tốc tại t = 20 s là v = 0 m/s.
Gia tốc của chuyển động là: a3 = \(\frac{{\Delta v}}{{\Delta t}}\)= \(\frac{{v - {v_{03}}}}{{\Delta t}}\)=\(\frac{{0 - 4}}{{20}}\)= -0,2 m/s2
Vận tốc của chuyển động là: \({v_3} = {v_{03}} + {a_3}t\)\( = \)\(4 - 0,2t\)(m/s).
Độ dịch chuyển của chuyển động: \({d_3} = {v_{03}}t + \frac{1}{2}{a_3}{t^2}\)\( = 4t - 0,1{t^2}\)(m).
b) Ta có độ dịch chuyển của chuyển động 3 sau 20 s chuyển động là:
\({d_3} = {v_{03}}t + \frac{1}{2}{a_3}{t^2}\)\( = 4t - 0,1{t^2}\)\( = {\rm{ }}4.20{\rm{ }} - {\rm{ }}0,{1.20^2} = {\rm{ }}40{\rm{ }}m.\)
-- Mod Vật Lý 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài tập 9.4 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.5 trang 15 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.7 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.8 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.9 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.10 trang 16 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.11 trang 17 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 9.12 trang 17 SBT Vật lý 10 Kết nối tri thức - KNTT