Để giúp các em ôn tập lại kiến thức cũ Hoc247 xin giới thiệu đến các em tài liệu Bộ 4 đề thi HK1 môn Toán 9 có đáp án năm 2021-2022 Trường THCS Nguyễn Trãi để các em tham khảo. Chúc các em học tập tốt và đạt kết quả cao trong học tập.
|
TRƯỜNG THCS NGUYỄN TRÃI |
ĐỀ THI HỌC KÌ I MÔN TOÁN 9 NĂM HỌC 2021 - 2022 |
ĐỀ 1
A. Trắc nghiệm (4đ)
Câu 1: Các so sánh nào sau đây sai?
A. Cos 32o > Sin 32o
B. Sin 65o = Cos 25o
C. Sin 45o < tan 45o
D. tan 30o = cot 30o
Câu 2: Tam giác ABC vuông tại A có AC = 6cm ; BC = 12cm. Số đo góc ACB bằng:
A. 30o
B. 45o
C. 60o
D. Đáp số khác
Câu 3: Dây cung AB = 12cm của đưong tròn (O;10cm) có khoảng cách đến tâm O là:
A. 5cm
B. 6cm
C. 7cm
D. 8cm
Câu 4: Cho đoạn thẳng OI = 6cm. Vẽ đường tròn (O;8cm) và (I; 2cm) . Hai đường tròn (O) và (I) có vị trí tương đối như thế nào?
A. Tiếp xúc ngoài
B. cắt nhau
C. tiếp xúc trong
D. đựng nhau
Câu 5: \(\sqrt {169} - 2\sqrt {49} + \sqrt {16} \)bằng:
A. -23
B. -4
C. 3
D. 17
Câu 6: Căn bậc hai số học của 81 là:
A. -9
B. 9
C. ±9
D. 81
Câu 7: Cho hàm số y = ax – 1 biết rằng khi x = -4 ; y = 3. vậy a bằng:
A. \(- \frac{3}{4}\)
B. \( \frac{3}{4}\)
C. 1
D. -1
Câu 8: Bán kính của đường tròn ngoại tiếp tam giác mà độ dài ba cạnh là 3cm, 4cm và 5cm là:
A. 1,5
B. 2
C. 2,5
D. 3
B. Tự luận (6đ)
Câu 1: (1.0 điểm)
Thực hiện phép tính:
\(5\sqrt {12} - 4\sqrt 3 + \sqrt {48} - 2\sqrt {75} \)
Câu 2: (2.0 điểm)
Cho biểu thức: \(A = \left( {\frac{{\sqrt x }}{{\sqrt x - 3}} + \frac{{\sqrt x }}{{\sqrt x + 3}}} \right):\left( {1 - \frac{3}{{\sqrt x + 3}}} \right)\)
a) Tìm điều kiện của x để A xác định.
b) Rút gọn A.
c) Tìm x để A = – 1 .
Câu 3: (3.0 điểm)
Cho (O) và điểm M nằm ngoài (O). Từ M kẻ 2 tiếp tuyến MA, MB sao cho góc AMB = 900 . Từ điểm C trên cung nhỏ AB kẻ tiếp tuyến (O) cắt MA, MB lần lượt ở P và Q Biết R = 10cm
a/ CMR Tứ giác AMBO là hình vuông
b/ Tính chu vi tam giác MPQ
c/ Tính góc POQ
ĐÁP ÁN
A. Trắc nghiệm
|
1D |
2C |
3D |
4C |
5C |
6B |
7D |
8C |
B. Tự luận
Câu 1:
\(\begin{array}{l}
{\rm{ }}5\sqrt {12} - 4\sqrt 3 + \sqrt {48} - 2\sqrt {75} \\
= 5\sqrt {4.3} - 4\sqrt 3 + \sqrt {16.3} - 2\sqrt {25.3} \\
= 10\sqrt 3 - 4\sqrt 3 + 4\sqrt 3 - 10\sqrt 3 = 0
\end{array}\)
Câu 2:
a/ Biểu thức A xác định khi x > 0 và x \( \ne \) 9
\(\begin{array}{l}
{\rm{b/ }}A = \left( {\frac{{\sqrt x }}{{\sqrt x - 3}} + \frac{{\sqrt x }}{{\sqrt x + 3}}} \right):\left( {1 - \frac{3}{{\sqrt x + 3}}} \right)\\
{\rm{ }} = \frac{{\sqrt x \left( {\sqrt x + 3} \right) + \sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}:\frac{{\left( {\sqrt x + 3} \right) - 3}}{{\sqrt x + 3}}\\
{\rm{ }} = \frac{{\sqrt x .2\sqrt x }}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} \cdot \frac{{\left( {\sqrt x + 3} \right)}}{{\sqrt x }} = \frac{{2\sqrt x }}{{\left( {\sqrt x - 3} \right)}}{\rm{ }}
\end{array}\)
.....
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
ĐỀ 2
A. Trắc nghiệm (3 đ)
Khoanh tròn vào chữ cái đứng trước khẳng định đúng trong các câu sau
Câu 1: \(\sqrt {21 - 7x} \) có nghĩa khi
A. x ≥ - 3
B. x ≤ 3
C. x > -3
D. x < 3.
Câu 2: Rút gọn các biểu thức \(3\sqrt {3a} + 4\sqrt {12a} - 5\sqrt {27a} \) (a ≥ 0) được
A. 4\(\sqrt {3a} \)
B. 26\(\sqrt {3a} \)
C. -26\(\sqrt {3a} \)
D. -4\(\sqrt {3a} \)
Câu 3: Giá trị biểu thức \(\sqrt {16} \cdot \sqrt {25} + \frac{{\sqrt {196} }}{{\sqrt {49} }}\) bằng
A. 28
B. 22
C.18
D. \(\sqrt 2 \)
Câu 4: Tìm x biết \(\sqrt[3]{x} = - 1,5\). Kết quả
A. x = -1,5
B.-3,375
C.3,375
D. ,25
Câu 5: Rút gọn biểu thức \(\sqrt[3]{{27{x^3}}} - \sqrt[3]{{8{x^3}}} + 4x\) được
A. 23
B. 23x
C. 15x
D. 5x
Câu 6: Rút gọn biểu thức \(\frac{2}{{\sqrt 7 - 3}} - \frac{2}{{\sqrt 7 + 3}}\) được
A. \(\sqrt 7 + 3\)
B. \(\sqrt 7 - 3\)
C.-6
D. 0
B. Tự luận (7 đ)
Câu 1: (1,5 điểm) Tìm x biết: \(2\sqrt {8x} + 7\sqrt {18x} = 9 - \sqrt {50x} \)
Câu 2: (2,5 điểm) Trên cùng một mặt phẳng tọa độ cho hai đường thẳng (d): y = x-3 và (d’): y = - 2x+3
a) Vẽ (d) và (d’) .
b) Bằng phép toán tìm tọa độ giao điểm của (d) và (d’)
Câu 3: (3 điểm) Cho đường tròn (O,R), điểm A nằm bên ngoài đường tròn, vẽ hai tiếp tuyến AB, AC với đường tròn (B và C là hai tiếp điểm) vẽ đường kính CD của đường tròn O. Chứng minh:
a. OA \( \bot \) BC
b. BD // OA
c. Cho R = 6 cm, AB = 8 cm. Tính BC
ĐÁP ÁN
A. Trắc nghiệm
|
1B |
2D |
3B |
4B |
5D |
6C |
B. Tự luận
Câu 1:
\(8\sqrt {8x} - 4\sqrt {18x} = 9 - \sqrt {50x} \) (đk x ≥ 0)
<=> \(16\sqrt {2x} - 12\sqrt {2x} = 9 - 5\sqrt {2x} \)
<=> \(16\sqrt {2x} - 12\sqrt {2x} + 5\sqrt {2x} = 9\)
<=> \(9\sqrt {2x} = 9\)
<=> \(\sqrt {2x} = 1\)
<=> \(x = \frac{1}{2}\)(n)
Vậy \(x = \frac{1}{2}\)
Câu 2:
a)
TXĐ: R
Xác định đúng 2 bảng giá trị
Vẽ đúng 2 đồ thị

.....
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
ĐỀ 3
A. Trắc nghiệm (3đ)
Câu 1: Giá trị của biểu thức \(\frac{1}{{2 + \sqrt 3 }} + \frac{1}{{2 - \sqrt 3 }}\) bằng
A. \(\frac{1}{2}\)
B. 1
C. 4
D. -4
Câu 2: Đường tròn là hình:
A. Không có trục đối xứng
B. Có một trục đối xứng
C. Có hai trục đối xứng
D. Có vô số trục đối xứng
Câu 3: Nếu hai đường thẳng y = -3x + 4 (d1) và y = (m+1)x + m (d2) song song với nhau thì m bằng
A. – 2.
B. -4
C. 4.
D. – 3.
Câu 4: Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng
A. 30.
B. 20.
C. 15.
D. 15 .
Câu 5: Điểm nào sau đây thuộc đồ thị hàm số y = - 3x + 2 là:
A. (-1;-1)
B. (-1;5)
C. (2;-8)
D. (4;-14)
Câu 6: Trên hình 1.2 ta có:
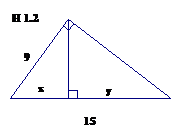
A. x = 5,4 và y = 9,6
B. x = 5 và y = 10
C. x = 10 và y = 5
D. x = 9,6 và y = 5,4
B. Tự luận (7đ)
Câu 1: ( 1,5 điểm): Rút gọn biểu thức
a) \(\sqrt 3 - 2\sqrt {48} + 3\sqrt {75} - 4\sqrt {108} \)
b) \(3\sqrt[3]{8} - \sqrt[3]{{27}} + \sqrt[3]{{64}}\)
Câu 2: ( 2 điểm): Cho hàm số y = -2x + 1 (d)
a)Vẽ đồ thị (d) của hàm số y = -2x + 1
b)Xác định các hệ số a và b của hàm số y = ax + b, biết rằng đồ thị của hàm số này song song với đồ thị (d) và đi qua điểm A(2; 1).
Câu 3: ( 3,5 điểm): Trên nửa đường tròn (O;R) đường kính BC, lấy điểm A sao cho BA = R.
a) Chứng minh tam giác ABC vuông tại A và tính số đo các góc B, C của tam giác vuông ABC.
b) Qua B kẻ tiếp tuyến với nửa đường tròn (O), nó cắt tia CA tại D. Qua D kẻ tiếp tuyến DE với nửa đường tròn (O) (E là tiếp điểm). Gọi I là giao điểm của OD và BE. Chứng minh rằng
c) Kẻ EH vuông góc với BC tại H. EH cắt CD tại G. Chứng minh IG song song với BC.
.....
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
ĐỀ 4
A. Trắc nghiệm (5đ)
Câu 1: Trong hệ tọa độ Oxy, đường thẳng y = 2 - x song song với đường thẳng:
A . y = -x
B . y = -x + 3
C . y = -1 - x
D . Cả ba đường thẳng trên
Câu 2. Nếu điểm B(1 ;-2) thuộc đường thẳng y = x – b thì b bằng:
A. -3
B. -1
C. 3
D. 1
Câu 3: Cho hai đường thẳng: (d) : y = 2x + m – 2 và (d’) : y = kx + 4 – m; (d) và (d’) trùng nhau nếu :
A. k = 2 và m = 3
B. k = -1 và m = 3
C. k = -2 và m = 3
D. k = 2 và m = -3
Câu 4: Góc tạo bởi đường thẳng và trục Ox có số đo là:
A. 450
B. 300
C. 600
D. 1350.
Câu 5: Hệ số góc của đường thẳng: là:
A. 4
B. -4x
C. -4
D. 9
Câu 6: Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm, BC = 15 cm . Tính độ dài AH là :
A. 8,4 cm
B. 7,2 cm
C. 6,8 cm
D. 4.2 cm
Câu 7: Tâm của đường tròn ngoại tiếp tam giác là giao điểm của các đường :
A. Trung tuyến
B. Phân giác
C. Đường cao
D. Trung trực
Câu 8: Hai đường tròn (O) và (O’) tiếp xúc ngoài.Số tiếp tuyến chung của chúng là:
A.1
B . 2
C . 3
D .4
Câu 9: Cho (O ; 6cm) và đường thẳng a có khoảng cách đến O là d, điều kiện để đường thẳng a là cát tuyến của đường tròn (O) là:
A. d<6 cm
B. d=6cm
C. d > 6cm
D. d 6cm
Câu 10: Dây AB của đường tròn (O; 5cm) có độ dài là 6 cm. Khoảng cách từ O đến AB bằng:
A. 6cm
B. 7 cm
C. 4 cm
D. 5 cm
B. Tự luận (5đ)
Câu 1: (1 điểm)Tính:
a) \(\sqrt 8 - 2\sqrt {32} + 3\sqrt {50}\)
b) \(\frac{1}{{3 + \sqrt 2 }} - \frac{1}{{3 - \sqrt 2 }}\)
Câu 2: (1,5 điểm) Cho hàm số y = (m + 1)x – 3. (m -1). Xác định m để :
a) Hàm số đã cho đồng biến, nghịch biến trên R.
b) Đồ thị hàm số song song với đường thẳng y = 2x. Vẽ đồ thị với m vừa tìm được.
Câu 3: (2,5 điểm) Cho đường tròn (O ; R) và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyến AB và AC (B,C là tiếp điểm). Kẻ đường kính BD.Đường thẳng vuông góc với BD tại O cắt đường thẳng DC tại E.
a) Chứng minh và DC // OA
b) Chứng minh tứ giác AEDO là hình bình hành.
c) Đường thẳng BC cắt OA và OE lần lượt tại I và K, chứng minh \IK.IC + OI.IA = {R^2}\)
ĐÁP ÁN
A. Trắc nghiệm
|
1D |
2C |
3A |
4A |
5C |
6B |
7D |
8C |
9A |
10C |
B. Tự luận
Câu 1:
a) \(\sqrt 8 - 2\sqrt {32} + 3\sqrt {50} = 2\sqrt 2 - 8\sqrt 2 + 15\sqrt 2 = 9\sqrt 2 \)
b) \(\frac{1}{{3 + \sqrt 2 }} - \frac{1}{{3 - \sqrt 2 }} = \frac{{3 - \sqrt 2 - 3 - \sqrt 2 }}{{\left( {3 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} = - 2\sqrt 2 \)
Câu 2:
Cho hàm số y = (m + 1)x – 3. (m -1). Xác định được m :
a) Hàm số đã cho đồng biến trên R khi m > -1
Hàm số nghịch biến trên R khi m < -1.
b) Đồ thị hàm số song song với đường thẳng y = 2x nên m + 1 = 2 và -3 0 suy ra m = 1(Thỏa mãn)
Vẽ được đồ thị hàm số y = 2x – 3:
-Cho x = 0 => y = -3 ta được điểm (0;-3) thuộc Oy.
-Cho y = 0 =>x = 1,5 ta được điểm (1,5 ;0) thuộc Ox.
Vẽ đường thẳng đi qua hai điểm trên ta được đồ thị hàm số y = 2x – 3.
........
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
Trên đây là một phần nội dung Bộ 4 đề thi HK1 môn Toán 9 có đáp án năm 2021-2022 Trường THCS Nguyễn Trãi. Để xem toàn bộ nội dung các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.
Chúc các em học tốt!