Bài tập 9 tr 100 sách BT Toán lớp 9 Tập 2
Cho \(C\) là một điểm nằm trên cung lớn \(AB\) của đường tròn \((O).\) Điểm \(C\) chia cung lớn \(\overparen{AB}\) thành hai cung \(\overparen{AC}\) và \(\overparen{CB}.\) Chứng minh rằng cung lớn \(\overparen{AB}\) có \(sđ \overparen{AB} = sđ \overparen{AC} = sđ \overparen{CB}.\)
Hướng dẫn: Xét \(3\) trường hợp:
\(a)\) Tia \(OC\) nằm trong góc đối đỉnh của góc ở tâm \(\widehat{AOB}.\)
\(b)\) Tia \(OC\) trùng với tia đối của một cạnh của góc ở tâm \(\widehat{AOB}.\)
\(c)\) Tia \(OC\) nằm trong một góc kề bù với góc ở tâm \(\widehat{AOB}.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của nửa đường tròn bằng \(180^o.\)
+) Số đo của cung lớn bằng hiệu giữa \(360^o\) và số đo cung nhỏ (có chung hai đầu mút với cung lớn).
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết
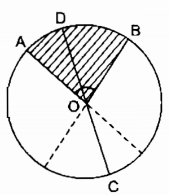
a) Trường hợp tia OC nằm trong góc đối đỉnh với \(\widehat {AOB}\)
Kẻ đường kính CD
Suy ra: OD nằm giữa OA và OB nên điểm D nằm trên cung nhỏ cung AB
\( \Rightarrow \) sđ cung AD (nhỏ) + sđ cung BD (nhỏ) = sđ cung AB (nhỏ) (1)
Vì OA nằm giữa OC và OD nên điểm A nằm trên cung nửa đường tròn CD.
\( \Rightarrow \) sđ cung AD (nhỏ) + sđ cung AC (nhỏ) = 1800 (2)
Vì OB nằm giữa OC và OD nên điểm B nằm trên cung nửa đường tròn CD.
\( \Rightarrow \) sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 1800 (3)
Cộng từng vế (2) và (3):
sđ cung AD (nhỏ) + sđ cung AC (nhỏ) + sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 3600 (4)
Từ (1) và (4) suy ra: sđ cung AC (nhỏ) + sđ cung BC (nhỏ) + sđ cung AB (nhỏ) = 3600
\( \Rightarrow \) sđ cung AC (nhỏ) + sđ cung BC (nhỏ) = 3600 - sđ cung AB (nhỏ)
Mà 3600 - sđ cung AB (nhỏ) = sđ cung AD (lớn)
Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC + sđ cung BC
b)
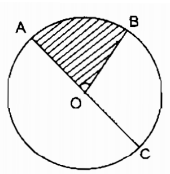
Trường hợp tia OC trùng với tia đối của một cạnh của góc ở tâm AOB ta có:
\(\widehat {AOB} + \widehat {BOC} = {180^0}\); $\widehat {AOC} = {180^0}\)
\( \Rightarrow \widehat {AOB} + \widehat {BOC} + \widehat {AOC} = {360^0}\)
\( \Rightarrow \widehat {AOC} + \widehat {BOC} = {360^0} - \widehat {AOB}\)
Suy ra: sđ cung AB + sđ cung BC (nhỏ) = 3600 - sđ cung AB (nhỏ)
Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC (nhỏ) + sđ cung BC
c)
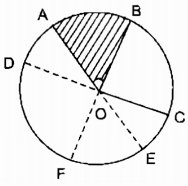
Trong hợp tia OC nằm trong góc kề bù với góc ở tâm AOB, kẻ đường kính AE.
Theo trường hợp b ta có:
sđ cung AB (lớn) = sđ cung AE (nhỏ) + sđ cung BE (nhỏ)
Ta xét trường hợp C nằm trên cung nhỏ EB:
sđ cung EB (nhỏ) = sđ cung EC (nhỏ) + sđ cung CB (nhỏ)
\( \Rightarrow \) sđ cung AB (lớn) = sđ cung AE + sđ cung EC (nhỏ) + sđ cung CB (nhỏ)
Theo kết quả trường hợp b ta có:
sđ cung AE + sđ cung EC (nhỏ)= sđ cung AC (lớn)
Vậy với cung AB lớn ta có: sđ cung AB = sđ cung AC + sđ cung CB
Trong trường hợp OC nằm trên góc đối với góc ở tâm \(\widehat {BOE}\) chứng minh tương tự.
Trong trường hợp OC nằm trên góc đối đỉnh với góc ở tâm \(\widehat {AOB}\) chứng minh ở trường hợp a.
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





