Bài tập 7 tr 99 sách BT Toán lớp 9 Tập 2
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A, B.\) Đường phân giác của góc \(OBO’\) cắt các đường tròn \((O),\) \( (O’)\) tương ứng tại \(C, D.\)
Hãy so sánh các góc ở tâm \(BOC\) và \(BO’D.\)
Hướng dẫn. Sử dụng các tam giác cân \(OBC,\) \(O’BD.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.
Lời giải chi tiết
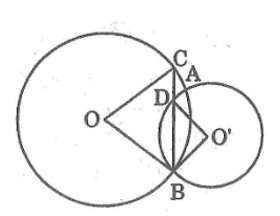
Trong \((O)\) ta có:
\(\Delta OBC\) cân tại \(O\) (vì \(OB = OC=\) bán kính)
\( \Rightarrow \widehat {BOC} = {180^0} - 2.\widehat {OBC}\; \;(1)\)
Trong \((O’)\) ta có:
\(\Delta BO'D\) cân tại \(O’\) (vì \(O’D = O’D=\) bán kính)
\( \Rightarrow \widehat {BO'D} = {180^0} - 2.\widehat {O'BD}\;\; (2)\)
Lại có \(\widehat {OBC} = \widehat {O'BD}\) \( (3)\) (vì \(BC\) là phân giác của \(\widehat {OBO'}\))
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {BOC} = \widehat {BO'D}\).
-- Mod Toán 9 HỌC247
-
Bài 1 trang 99 sách bài ập toán 9 tập 2
bởi Nguyễn Lệ Diễm
10/10/2018
Bài 1 (Sách bài tập - tập 2 - trang 99)a) Từ 1 giờ đến 3 giờ thì kim giờ quay được một góc ở tâm bằng bao nhiêu độ ?
b) Cũng hỏi như thế từ giờ đến 6 giờ ?
Theo dõi (0) 1 Trả lời
