Bài tập 1.2 tr 100 sách BT Toán lớp 9 Tập 2
Cho đường tròn tâm \(O\) đường kính \(AB.\) Các điểm \(C, D, E\) cùng thuộc một cung \(AB\) sao cho \(sđ \overparen{BC} =\dfrac{1}{6} sđ \overparen{BA};\) \( sđ \overparen{BD} = \displaystyle{1 \over 2} sđ \overparen{BA};\)\( sđ \overparen{BE} =\displaystyle{2 \over 3} sđ \overparen{BA}.\)
\(a)\) Đọc tên các góc ở tâm có số đo không lớn hơn \(180^o.\)
\(b)\) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
\(c)\) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn \(180^o\)).
\(d)\) So sánh hai cung nhỏ \(AE\) và \(BC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
+) Cung nhỏ có số đo nhỏ hơn \(180^o.\)
Lời giải chi tiết
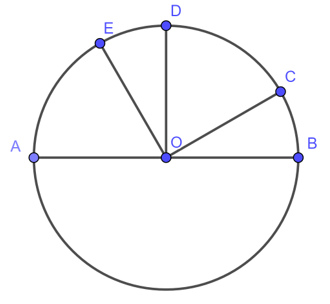
\(a)\) Các góc ở tâm có số đo không quá \(180^o\) là:
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {AOE},\widehat {BOC},\)\(\widehat {BOD},\)\(\widehat {BOE},\widehat {COD},\widehat {COE},\widehat {DOE}\)
\(b)\) Ta có: \(\widehat {AOB} = {180^0}\)
\(\Rightarrow sđ \overparen{AB} = 180^o\)
Ta có: \(sđ \overparen{BC}= \displaystyle{1 \over 6} sđ \overparen{AB}\)
\(=\displaystyle {1 \over 6}{.180^0}= 30^o\)
\( \Rightarrow \widehat {BOC} = sđ \overparen{BC}= 30^o\)
Ta có: sđ \(\overparen{BD} =\displaystyle {1 \over 2} sđ \overparen{AB}\)
\(=\displaystyle{1 \over 2}{.180^0} = {90^0}\)
\( \Rightarrow \widehat {BOD} = sđ \overparen{BD} = {90^0}\)
Ta có: \(sđ \overparen{BE} = \displaystyle{2 \over 3} sđ \overparen{BA}\)
\( = \displaystyle{2 \over 3}{.180^0} = {120^0}\)
\( \Rightarrow \widehat {BOE} = sđ \overparen{BE}= 120^o\)
\(\widehat {BOC} + \widehat {COE} = \widehat {BOE}\)
\( \Rightarrow \widehat {COE} = \widehat {BOE} - \widehat {BOC}\)
\( = {120^0} - {30^0} = {90^0}\)
\(\widehat {AOE} + \widehat {BOE} = \widehat {AOB}\)
\( \Rightarrow \widehat {AOE} = \widehat {AOB} - \widehat {BOE}\)
\( = {180^0} - {120^0} = {60^0}\)
\(\widehat {AOD} = \widehat {BOD} = \displaystyle{1 \over 2}\widehat {AOB} = {90^0}\)
\(\widehat {BOC} + \widehat {COD} = \widehat {BOD}\)
\( \Rightarrow \widehat {COD} = \widehat {BOD} - \widehat {BOC}\)
\(={90^0} - {30^0} = {60^0}\)
\(\widehat {COD} + \widehat {DOE} = \widehat {COE}\)
\( \Rightarrow \widehat {DOE} = \widehat {COE} - \widehat {COD}\)
\( = {90^0} - {60^0} = {30^0}\)
\(\widehat {COA} + \widehat {BOC} = 180^0\)
\( \Rightarrow \widehat {AOC} = 180^0 - \widehat {BOC}\)
\( = {180^0} - {30^0} = {150^0}\)
\(c)\) Các cung có số đo nhỏ hơn \(180^o\) bằng nhau.
\(\overparen{BC}=\overparen{DE}\); \(\overparen{AE}=\overparen{CD}\); \(\overparen{AD}=\overparen{BD}\); \(\overparen{AD}=\overparen{CE}\); \(\overparen{CE}=\overparen{BD}\).
\(d)\) \(sđ\overparen{AE} = \widehat {AOE} = {60^0}\)
\(sđ \overparen{BC} = \widehat {BOC} = {30^0}\)
Ta có số đo của cung \(\overparen{AE}\) gấp đôi số đo của cung \(\overparen{BC}\).
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





