Bài tập 71 trang 113 SBT Toán 9 Tập 2

23 BT SGK

Bài tập 71 tr 113 sách BT Toán lớp 9 Tập 2

Trong một tam giác đều \(ABC\; (h.13),\) vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng \(a,\) tính diện tích hình hoa thị gạch sọc.

Hình học 9 Bài 10 Trắc nghiệm Hình học 9 Bài 10 Giải bài tập Hình học 9 Bài 10

Hướng dẫn giải chi tiết

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}\).

Lời giải chi tiết

Diện tích hình hoa thị bằng tổng diện tích \(3\) hình viên phân trừ diện tích tam giác đều \(ABC.\)

Gọi \(O\) là tâm của tam giác đều \(ABC\)

\( \Rightarrow OA = OB = OC\)

Vì \(∆ABC\) đều nên \(AO,\) \(BO,\) \(CO\) là phân giác của các góc \(\widehat A,\widehat B,\widehat C\)

\(\widehat {OAC} = \widehat {OCA} = \displaystyle {{{{60}^\circ}} \over 2} = {30^\circ}\)

\(\widehat {AOC} = {180^\circ} - \left( {{{30}^\circ} + {{30}^\circ}} \right) = {120^\circ}\)

Trong tam giác \(O’HA\) có \(\widehat {O'HA} = {90^\circ}\), \(\widehat {HO'A} = {60^\circ}\)

\(AH = R.\sin \widehat {HO'A}\)\( = R. \sin 60^\circ= \displaystyle {{R\sqrt 3 } \over 2}\)

\(AC=2AH=R\sqrt 3 \)

\( \Rightarrow R =\displaystyle {\displaystyle {AC} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} = {{a\sqrt 3 } \over 3}\)

\(S_{quạt}=\displaystyle {{\pi \displaystyle {{\left( {{\displaystyle {a\sqrt 3 } \over 3}} \right)}^2}.120} \over {360}}\)

\(=\displaystyle {{\pi \displaystyle {{\displaystyle {a^2}} \over 3}} \over 3} = {{\pi {a^2}} \over 9}\) (đơn vị diện tích)

\(∆O'HA\) có \(\widehat {O'HA} = {90^\circ}\); \(\widehat {HO'A} = {60^\circ}\)

\(O'A=R.\cos {60^\circ} = \displaystyle {{a\sqrt 3 } \over 3}.{1 \over 2} = {{a\sqrt 3 } \over 6}\)

\(S_{\Delta O'CA}=\displaystyle {1 \over 2}O'H.AC \)\(\displaystyle = {1 \over 2}.{{a\sqrt 3 } \over 6}.a = {{{a^2}\sqrt 3 } \over {12}}\) (đơn vị diện tích)

Diện tích hình viên phân:

\(S_{vp}=S_{quạt}-S_{\Delta O'CA}\) \(= \displaystyle {{\pi {a^2}} \over 9} - {{{a^2}\sqrt 3 } \over {12}} = {{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {36}}\)

Diện tích tam giác đều \(ABC\) cạnh \(a:\) \(S_{ABC}= \dfrac{a^2\sqrt 3 } {4}\) (đơn vị diện tích)

Diện tích hình hoa thị là:

\(S=3S_{vp}-S_{ABC}\)\(= \displaystyle 3.{{4\pi {R^2} - 3{a^2}\sqrt 3 } \over {36}} - {{{a^2}\sqrt 3 } \over 4}\)

\(= \displaystyle {{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {12}} - {{3{a^2}\sqrt 3 } \over {12}}\)

\(= \displaystyle {{4\pi {a^2} - 6{a^2}\sqrt 3 } \over {12}} = {{{a^2}} \over 6}\left( {2\pi - 3\sqrt 3 } \right)\) (đơn vị diện tích)

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 71 trang 113 SBT Toán 9 Tập 2 HAY thì click chia sẻ

Nêu cách vẽ hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1CM

bởi bach dang 08/10/2018

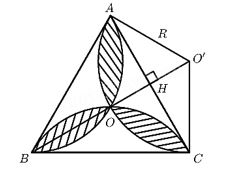
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1 cm. Nêu cách vẽ.

b) Tính diện tích miền gạch sọc.

Bài tập 71 trang 113 SBT Toán 9 Tập 2

23 BT SGK

Hướng dẫn giải chi tiết

Nêu cách vẽ hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1CM