Bài tập 10.2 tr 113 sách BT Toán lớp 9 Tập 2
Tính diện tích của hình cánh hoa, biết \(OA = R (h.bs.8).\)
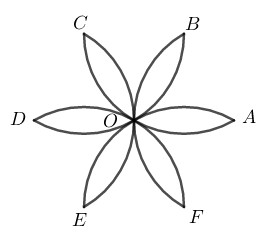
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong đường tròn \(R,\) độ dài \(l\) của một cung \(n^\circ\) được tính theo công thức: \(l=\dfrac{\pi Rn}{180}.\)
+) Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}\) hay \(S=\dfrac{lR}{2}\)
Lời giải chi tiết
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung \(\overparen{BO}\) và dây căng cung đó thì cung \(\overparen{BO}\) là cung của đường tròn tâm A bán kính R.
OA = AB = OB = R
\( \Rightarrow \Delta AOB\) đều \( \Rightarrow \widehat {OAB} = {60^0}\)
Squạt OAB = \({{\pi {R^2}.60} \over {360}} = {{\pi {R^2}} \over 6}\)
.jpg)
Kẻ \(AI \bot BO\). Trong tam giác vuông AIO ta có:
AI = AO. sin\(\widehat {AOI} = R.\sin {60^0} = {{R\sqrt 3 } \over 2}\)
S∆AOB =\({1 \over 2}AI.AB = {1 \over 2}.{{R\sqrt 3 } \over 2}.R = {{{R^2}\sqrt 3 } \over 4}\)
Diện tích 1 hình viên phân là:
S1 = Squạt OAB – S AOB
=\({{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {{2\pi {R^2} - 3{R^2}\sqrt 3 } \over {12}}\)
Diện tích của hình cánh hoa:
S = 12. S1 = 12.\({{2\pi {R^2} - 3{R^2}\sqrt 3 } \over {12}} = {R^2}\left( {2\pi - 3\sqrt 3 } \right)\) (đơn vị diện tích)
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





