Bài tập 27 trang 104 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

+) Nếu các tia \(Oy\) và \(Oz\) thuộc cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) và \(\widehat{xOy}=\widehat{xOz}\) thì tia \(Oy\) và \(Oz\) trùng nhau.

Lời giải chi tiết

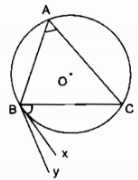
∆ABC nội tiếp trong đường tròn (O) có ba khả năng xảy ra của tam giác

- ∆ABC là tam giác nhọn

- ∆ABC là tam giác vuông

- ∆ABC là tam giác tù

Xét trường hợp ∆ABC là tam giác nhọn

Giả sử Bx không phải là tiếp tuyến của đường tròn (O). Trên cùng nửa mặt phẳng bờ đường thẳng BC chứa tia Bx ta kẻ tia By là tiếp tuyến của đường tròn (O)

\( \Rightarrow \widehat {CBy} = \widehat {BAC}\) (hệ quả của góc giữa tia tiếp tuyến và dây cung)

\(\widehat {CBx} = \widehat {BAC}\) (gt)

Suy ra: \(\widehat {CBy} = \widehat {CBx}\)

Ta có By và  Bx là hai tia khác nhau từ nằm trên cùng một nửa mặt phẳng bờ BC tạo với BC một góc bằng nhau với tính chất đặt tia trên nửa mặt phẳng. Mâu thuẫn với giả sử Bx không phải là tiếp tuyến của đường tròn (O). Vậy Bx là tiếp tuyến của đường tròn (O).

-- Mod Toán 9 HỌC247