Phần hướng dẫn giải bài tập Hình học 8 Bài 6 Trường hợp đồng dạng thứ nhất sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình học 8 Tập 2
-
Bài tập 32 trang 77 SGK Toán 8 Tập 2
Trên một cạnh của góc xOy\((\widehat{xOy}=180^0)\), Đặt các đoạn thẳng OA= 5cm, OB= 16cm. Trên cạnh thứ hai của góc đó, đặt các đoạn OC= 8cm, OD= 10cm.
a) Chứng minh hai tam giác OCB và OAD đồng dạng.
b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có góc các góc bằng nhau từng đôi một.
-
Bài tập 33 trang 77 SGK Toán 8 Tập 2
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k, thì hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng k.
-
Bài tập 34 trang 77 SGK Toán 8 Tập 2
Dựng tam giác \(ABC\), biết \(\widehat{A}={60^o}\) và, tỉ số \(\dfrac{AB}{AC} = \dfrac{4}{5}\) và đường cao \(AH = 6cm\).
-
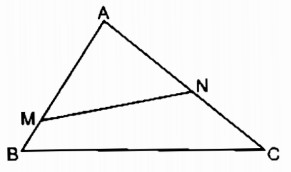
Bài tập 35 trang 92 SBT Toán 8 Tập 2
Cho tam giác ABC có AB = 12cm, AC = 15cm, BC = 18cm.
Trên cạnh AB, đặt đoạn thẳng AM = 10cm, trên cạnh AC đặt đoạn thẳng AN = 8cm. Tính độ dài đoạn thẳng MN.
-
Bài tập 36 trang 92 SBT Toán 8 Tập 2
Hình thang \(ABCD \;(AB // CD)\) có \(AB = 4cm, CD = 16cm\) và \(BD = 8cm \) (h23).
Chứng minh \(\widehat {BAD} = \widehat {DBC}\) và \(BC = 2 AD.\)
-
Bài tập 37 trang 92 SBT Toán 8 Tập 2
Cho tam giác ABC có \(\widehat A = 60^\circ \) , AB = 6cm, AC = 9cm
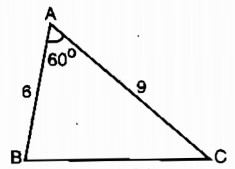
a. Dựng tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k = \({1 \over 3}\)
b. Hãy nêu một vài cách dựng khác và vẽ hình trong từng trường hợp cụ thể.
-
Bài tập 38 trang 92 SBT Toán 8 Tập 2
Cho tam giác ABC có AB = 10cm, AC = 20cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm.
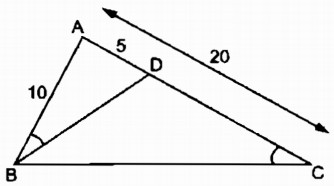
Chứng minh \(\widehat {ABD} = \widehat {ACB}\).
-
Bài tập 6.1 trang 92 SBT Toán 8 Tập 2
Hình bs.4 cho biết Oz là phân giác của góc xOy, OA = 9cm, OB = 12cm, OC = 16cm, AB = 6cm.
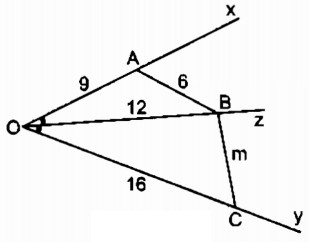
Độ dài của đoạn thẳng BC là m bằng:
A. 7,5cm
B. 8cm
C. 8,5cm
D. 9cm
Hãy chọn kết quả đúng.
-
Bài tập 6.2 trang 93 SBT Toán 8 Tập 2
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB.
a. Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng \(\widehat {ABE} = \widehat {ACB}\).
b. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.






