Giải bài 36 tr 92 sách BT Toán lớp 8 Tập 2
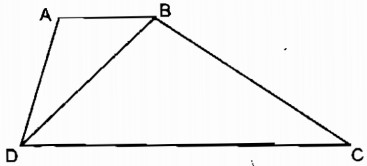
Hình thang \(ABCD \;(AB // CD)\) có \(AB = 4cm, CD = 16cm\) và \(BD = 8cm \) (h23).
Chứng minh \(\widehat {BAD} = \widehat {DBC}\) và \(BC = 2 AD.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng.
Lời giải chi tiết
Ta có:
\(\eqalign{ & {{AB} \over {BD}} = {4 \over 8} = {1 \over 2} \cr & {{BD} \over {DC}} = {8 \over {16}} = {1 \over 2} \cr} \)
\( \Rightarrow\displaystyle {{AB} \over {BD}} = {{BD} \over {DC}} = {1 \over 2}\)
Vì \(AB//CD\) (gt) nên \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(∆ ABD\) và \(∆ BDC\) có:
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
\(\displaystyle{{AB} \over {BD}} = {{BD} \over {DC}}\) (chứng minh trên)
\( \Rightarrow ∆ ABD\) đồng dạng \( ∆ BDC\) (c.g.c)
\( \Rightarrow \widehat {BAD} = \widehat {DBC}\) (hai góc tương ứng).
Tỉ số đồng dạng \(\displaystyle k = {AB \over BD}= {1 \over 2}\).
\( \Rightarrow\displaystyle {{AD} \over {BC}} = {1 \over 2} \Rightarrow BC = 2AD\) (đpcm).
-- Mod Toán 8 HỌC247
-


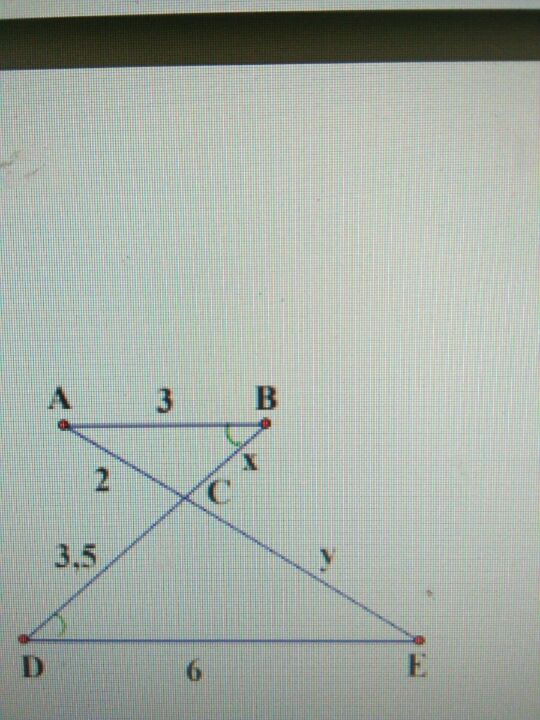
Tính các độ dài x, y trên hình vẽ
bởi Tran Thi Nhat Bang
 29/04/2020
29/04/2020
 Theo dõi (2) 4 Trả lời
Theo dõi (2) 4 Trả lời -


Cho tam giác ABC có ba góc nhọn , đường cao AH . Kẻ HD vuông góc AB tại D , HE vuông góc AC tại E
bởi TẬP BÀI
 14/04/2020
14/04/2020
(1) chứng minh tam giác AHB đồng dạng tam giác ADH , tam giác AHC đồng dạng với tam giác AEH
(2 ) chứng minh AD × AB = AE × AC ) .
( 3 ) cho AB = 12, HC= 15 , BC= 18 . TÍNH ĐỘ DÀI ĐƯỜNG PHÂN GIÁC AK BẾT AK THUỘC BC
Theo dõi (0) 0 Trả lời -


Chứng minh tam giác CHM đồng dạng với tam giác AHN?
bởi Đồng Thủy
 12/04/2020
12/04/2020
Giúp mình với
Cho tam giác abc vuông tại a kẻ đường cao AH có M là trung điểm của AH, N là trung điểm của HB chứng minh tam giác CHM đồng dạng với tam giác AHN
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời





