Giải bài 6.2 tr 93 sách BT Toán lớp 8 Tập 2
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB.
a. Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng \(\widehat {ABE} = \widehat {ACB}\).
b. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng.
- Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Trong tam giác cân, đường phân giác ứng với cạnh đáy đồng thời là đường cao, đường trung tuyến, đường trung trực của cạnh đáy.
Lời giải chi tiết
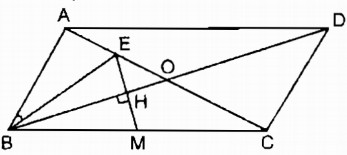
a) Vì \(ABCD\) là hình bình hành nên \(\displaystyle AO = CO = {1 \over 2}AC\)
\(BE\) là trung tuyến của tam giác \(ABO\) nên \(\displaystyle AE = {1 \over 2}AO\)
Mặt khác, \( AC = 2AB \) (gt) nên \(AB = AO\) do đó \(\displaystyle AE = {1 \over 2}AB\)
Xét \(\Delta AEB\) và \(\Delta ABC\) có:
\(\widehat A\) chung
\(\displaystyle {{AE} \over {AB}} = {{AB} \over {AC}} = {1 \over 2}\)
\( \Rightarrow ∆ AEB\) đồng dạng \(∆ ABC\) (c.g.c)
\( \Rightarrow \widehat {ABE} = \widehat {ACB}\) (hai góc tương ứng).
b) Theo chứng minh ở câu a) \(∆ AEB\) đồng dạng \(∆ ABC\) theo tỉ số \(\displaystyle k = {1 \over 2}\) nên ta có \(\displaystyle BE = {1 \over 2}BC\) hay \(\displaystyle BE = BM={1 \over 2}BC\) (vì \(M\) là trung điểm của \(BC\))
\( \Rightarrow ∆ BEM\) cân tại \(B.\)
Xét \(∆EBC \) có \(\displaystyle {{BE} \over {BC}} = {{OE} \over {OC}} = {1 \over 2}\)
\( \Rightarrow BO \) là đường phân giác góc \(EBC\).
Xét tam giác \(BEM\) cân tại \(B\) có \(BO\) là đường phân giác nên \(BO\) đồng thời là đường cao ứng với cạnh đáy \(EM\).
Vậy \(EM\bot \,BD\).
-- Mod Toán 8 HỌC247
-


Cho hình tam giác ABC (AB < AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE: F là giao điểm của AH và BC.
a) Chứng minh: AF \(\perp\) BC và \(\overline{AFD}\) = \(\overline{ACE}\) .
b) Gọi M là trung điểm của AH. Chứng minh: MD \(\perp\) OD và 5 điểm M, D, O, F, E cùng thuộc một đường tròn.
c) Gọi K là giao điểm của AH và DE. Chứng minh MD2 = MK.MF và K là trực tâm của tam giác MBC.
d) Chứng minh: \(\frac{2}{FK}\) = \(\frac{1}{FH}\) + \(\frac{1}{FA}\) .
Theo dõi (0) 1 Trả lời






