Vận dụng 2 trang 75 SGK Toán 7 Kết nối tri thức tập 2
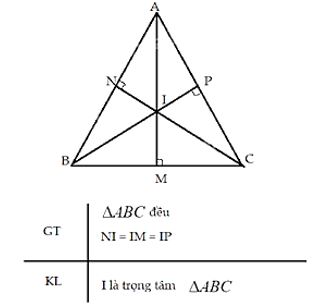
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Hướng dẫn giải chi tiết Vận dụng 2 trang 75
Phương pháp giải
Sử dụng tính chất trong tam giác cân.
Lời giải chi tiết
Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 3 trang 74 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 75 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.20 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.21 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.22 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.23 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.24 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.25 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.14 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.15 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.15 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.16 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.17 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.18 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT