Giải bài 9.12 trang 69 SGK Toán 7 Kết nối tri thức tập 2
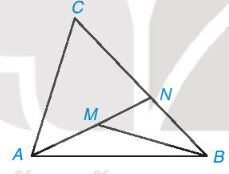
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC. (H.9.18)
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB
b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB
c) Chứng minh MA + MB < CA + CB.
Hướng dẫn giải chi tiết Giải bài 9.12
Phương pháp giải
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
Lời giải chi tiết
a) 3 điểm M,N,B không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác MNB có:
MB < MN + NB
MA + MB < MA + MN + NB
MA + MB < NA + NB ( vì MA + MN = NA) (1)
b) 3 điểm A,N,C không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác ACN có:
NA < CA + CN
NA + NB < CA + CN + NB
NA + NB < CA + CB ( vì CN + NB = CB) (2)
c) Từ (1) và (2) ta có:
MA + MB < NA + NB < CA + CB
Vậy MA + MB < CA + CB
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 9.10 trang 69 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.11 trang 69 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.13 trang 69 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.10 trang 52 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.11 trang 52 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.12 trang 52 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.13 trang 52 SBT Toán 7 Kết nối tri thức tập 2 - KNTT