Giải bài 10 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2
Cho hình hộp chữ nhật có thể tích bằng \(V = 3{x^3} + 8{x^2} - 45x - 50\) (cm3), chiều dài bằng \(\left( {x + 5} \right)\) cm và chiều cao \(\left( {x + 1} \right)\) cm. Hãy tính chiều rộng của hình hộp chữ nhật.
Hướng dẫn giải chi tiết Bài 10
Phương pháp giải
Thể tích của hình hộp chữ nhật là tích của ba kích thước.
Chiều rộng bằng thể tích chia cho tích của chiều dài và chiều cao
Lời giải chi tiết
Ta có chiều rộng được tính bởi phép tính:
\(\left( {3{x^3} + 8{x^2} - 45x - 50} \right):\left[ {\left( {x + 5} \right)\left( {x + 1} \right)} \right] = \left( {3{x^3} + 8{x^2} - 45x - 50} \right):\left( {{x^2} + 6x + 5} \right)\)
Ta có
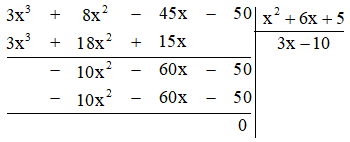
Vậy chiều rộng của hình chữ nhật là \(3x - 10\) cm.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





