Hướng dẫn Giải bài tập Toán 7 Kết nối tri thức Chương 4 Luyện tập chung trang 74 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Giải bài 4.16 trang 74 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
-
Giải bài 4.17 trang 74 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\) Tính độ dài cạnh DF.
-
Giải bài 4.18 trang 74 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
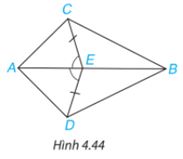
Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:
\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)
-
Giải bài 4.19 trang 74 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).
b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).