Giải bài 4.19 trang 74 SGK Toán 7 Kết nối tri thức tập 1
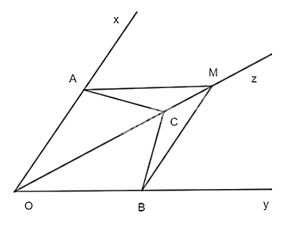
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).
b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).
Hướng dẫn giải chi tiết Giải bài 4.19
Phương pháp giải
a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.
Lời giải chi tiết
a)
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(\widehat {AOC} = \widehat {AOB}\)(Oz là phân giác góc xOy)
OC chung
\(\widehat {CAO} = \widehat {CBO}.\)
\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)
b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)
Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù
\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù
Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)
Xét \(\Delta MAC\) và \(\Delta MBC\) có:
AC=BC
\(\widehat {ACM} = \widehat {BCM}\)
CM chung
\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.