Bài tập 29 trang 90 SBT Toán 6 Tập 2
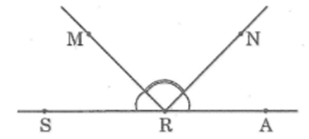
a) Vẽ vào vở hình dưới trong đó ba điểm S, R, A thẳng hàng và \(\widehat {ARM}\) = \(\widehat {SRN}\) = 1300
b) Tính \(\widehat {ARN}\), \(\widehat {MRS}\), \(\widehat {MRN}\)
c) Dùng thước đo góc kiểm tra lại kết quả
Hướng dẫn giải chi tiết
Hình vẽ như hình trên
Vì A,R, S thẳng hàng nên:
\(\begin{array}{l}
\widehat {ARN} + \widehat {RNS} = {180^0}\\
\Rightarrow \widehat {ARN} = {180^0} - \widehat {RNS}\\
= {180^0} - {130^0} = {50^0}
\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}
\widehat {ARM} + \widehat {MRS} = {180^0}\\
\Rightarrow \widehat {MRS} = {180^0} - \widehat {ARM}\\
= {180^0} - {130^0} = {50^0}
\end{array}\)
Dựa vào hình vẽ, ta có: \(\widehat {ARN} + \widehat {NRM} = \widehat {ARM}\)
Suy ra:
\(\begin{array}{l}
\widehat {MRN} = \widehat {ARM} - \widehat {ARN}\\
= {180^0} - {50^0} = {130^0}
\end{array}\)
-- Mod Toán 6 HỌC247
-


Chọn phát biểu sai trong các phát biểu sau:
bởi Lê Gia Bảo
 27/05/2020
27/05/2020
A. Nếu tia Ot là tia phân giác của ∠xOy thì tia Ot nằm giữa hai tia Ox, Oy
B. Nếu tia Ot là tia phân giác của ∠xOy thì ∠xOt = ∠yOt = ∠xOy/2
C. Nếu ∠xOt = ∠yOt thì tia Ot là tia phân giác của ∠xOy
D. Nếu ∠xOt = ∠yOt và tia Ot nằm giữa hai tia Ox, Oy thì tia Ot là tia phân giác của ∠xOy
Theo dõi (0) 1 Trả lời -


Cho đường thẳng xx' và một điểm O nằm trên đường thẳng ấy. Trên hai nửa mặt phẳng đối nhau bờ là đường thẳng xx', lấy hai điểm A, B sao cho ∠x'OA = 150° và ∠BOx = 30°. Chứng tỏ Ox là tia phân giác của góc ∠AOB ?
bởi Nguyễn Thanh Trà
 27/05/2020
Theo dõi (0) 1 Trả lời
27/05/2020
Theo dõi (0) 1 Trả lời -


Cho tia Ox. Vẽ hai góc xOy và xOz trên cùng nửa mặt phẳng bờ chứa tia Ox sao cho ∠xOy = 30°, ∠xOz = 45°. Trong ba tia Ox, Oy, Oz thì tia nào nằm giữa hai tia còn lại?
bởi Lê Gia Bảo
 27/05/2020
Theo dõi (0) 1 Trả lời
27/05/2020
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 24 trang 89 SBT Toán 6 Tập 2
Bài tập 25 trang 89SBT Toán 6 Tập 2
Bài tập 26 trang 89 SBT Toán 6 Tập 2
Bài tập 27 trang 89 SBT Toán 6 Tập 2
Bài tập 28 trang 189 SBT Toán 6 Tập 2
Bài tập 5.1 trang 90 SBT Toán 6 Tập 2
Bài tập 5.2 trang 90 SBT Toán 6 Tập 2
Bài tập 5.3 trang 90 SBT Toán 6 Tập 2
Bài tập 24 trang 84 SGK Toán 6 Tập 2
Bài tập 25 trang 84 SGK Toán 6 Tập 2
Bài tập 26 trang 84 SGK Toán 6 Tập 2
Bài tập 27 trang 85 SGK Toán 6 Tập 2