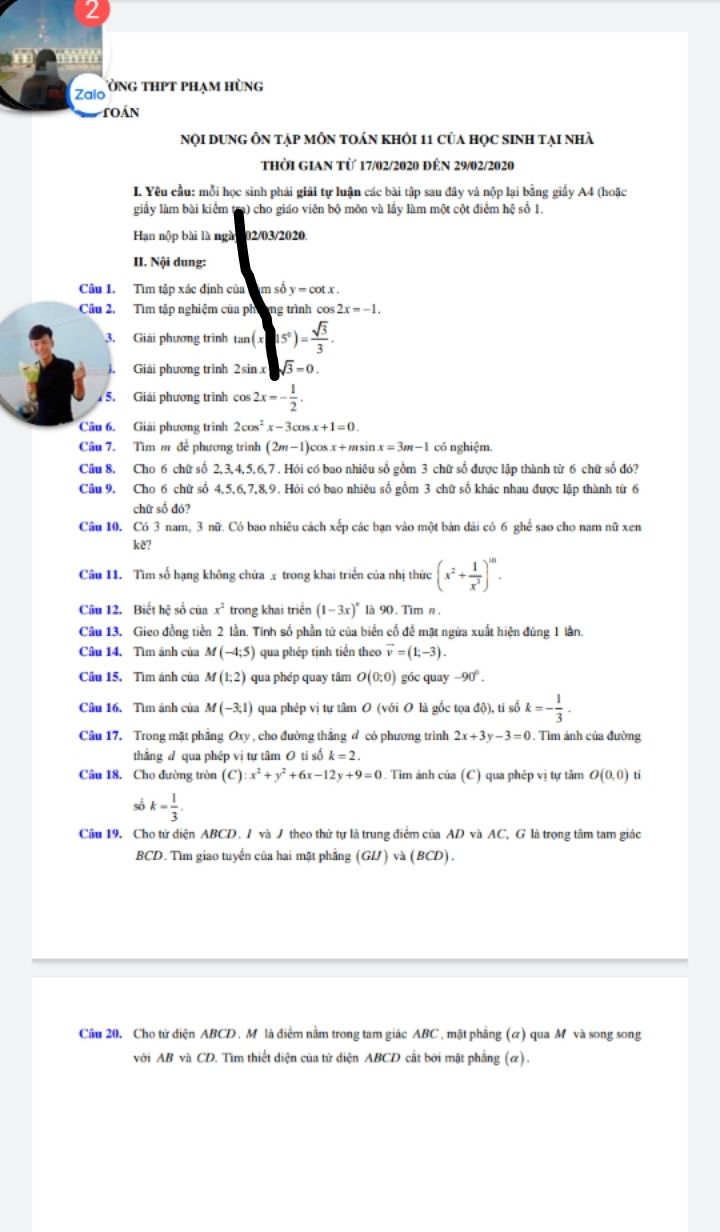
Giải bài 2.24 tr 76 SBT Toán 11
a) Một lớp có 50 học sinh. Tính số cách phân công 4 bạn quét sân trường và 5 bạn xén cây bằng hai phương pháp để rút ra đẳng thức \(C_{50}^9.C_9^4 = C_{50}^4.C_{46}^5\)
b) Chứng minh công thức Niu-tơn \(C_n^r.C_r^k = C_n^k.C_{n - k}^{r - k}\,\,\left( {n \ge r \ge k \ge 0} \right)\)
c) Tìm chữ số ở hàng đơn vị của tổng
S = 0!+2!+4!+6!+...+100!.
Hướng dẫn giải chi tiết
a) Cách 1: Chọn 9 bạn nam trong 50 bạn để làm trực nhật. Có \(C_{50}^9\) cách.
Khi đã chọn được 9 bạn rồi, chọn 4 trong 9 bạn đó để quét sân. Có \(C_9^4\) cách.
Từ đó, theo quy tắc nhân, có \(C_{50}^9.C_9^4\) cách phân công.
Cách 2: Chọn 4 trong 50 bạn để quét sân, sau đó chọn 5 trong 46 bạn còn lại để xén cây. Vậy có \(C_{50}^4.C_{46}^5\) cách phân công.
Từ đó ta có đẳng thức cần chứng minh.
b) Ta có: \(VT = C_n^rC_r^k = \frac{{n!}}{{r!(n - r)!}}\frac{{r!}}{{k!(r - k)!}} = \frac{{n!}}{{(n - r)!k!(r - k)!}}\)
\(\begin{array}{l}
VT = C_n^kC_{n - k}^{r - k} = \frac{{n!}}{{k!(n - k)!}}\frac{{(n - k)!}}{{(r - k)![n - k - (r - k)]!}}\\
= \frac{{n!}}{{k!(n - k)!}}\frac{{(n - k)!}}{{(r - k)!(n - r)!}}\\
= \frac{{n!}}{{k!(r - k)!(n - r)!}} = VT
\end{array}\)
c) Ta có: \(0! = 1,2! = 2,4! = 1.2.3.4 = 24,6! = 1.2.3.4.5.6 = 720\) (tận cùng là 0);...
Tương tự với các số hạng tiếp theo ta có các số hạng 6!; 8!;...100! đều có tận cùng là chữ số 0. Vì trong biểu thức khai triển tính giai thừa có 4×5 = 20 (tận cùng là 0). Do đó chữ số ở hàng đơn vị của S là 1+2+4 = 7.
-- Mod Toán 11 HỌC247
-


Gieo đồng tiền hai lần, tính số phần tử của biến cố để mặt ngử xuất hiện đúng 1 lần?
bởi Huy Hoang Phan
 26/03/2020
26/03/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính tổng của tất cả các số có năm chữ số đôi một khác nhau được thành lập từ tập A = {1;2;3;4;5}
bởi Kokoro
 09/02/2020
Tính tổng của tất cả các số có năm chữ số đôi một khác nhau được thành lập từ tập A = {1;2;3;4;5}Theo dõi (0) 2 Trả lời
09/02/2020
Tính tổng của tất cả các số có năm chữ số đôi một khác nhau được thành lập từ tập A = {1;2;3;4;5}Theo dõi (0) 2 Trả lời -


Có bao nhiêu số tự nhiên có 5 chữ số chia hết cho 11 mà các chữ số hàng đơn vị bằng 9?
bởi Cúc Nguyễn Thanh
 14/01/2020
Giúp e câu 40 vs ạ
14/01/2020
Giúp e câu 40 vs ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Có bao nhiêu số tự nhiên có 5 chữ số chia hết cho 11 mà có chữ số hàng đơn vị bằng 9?
bởi Cúc Nguyễn Thanh
 14/01/2020
Giúp e câu 40 vs ạ!!
14/01/2020
Giúp e câu 40 vs ạ!!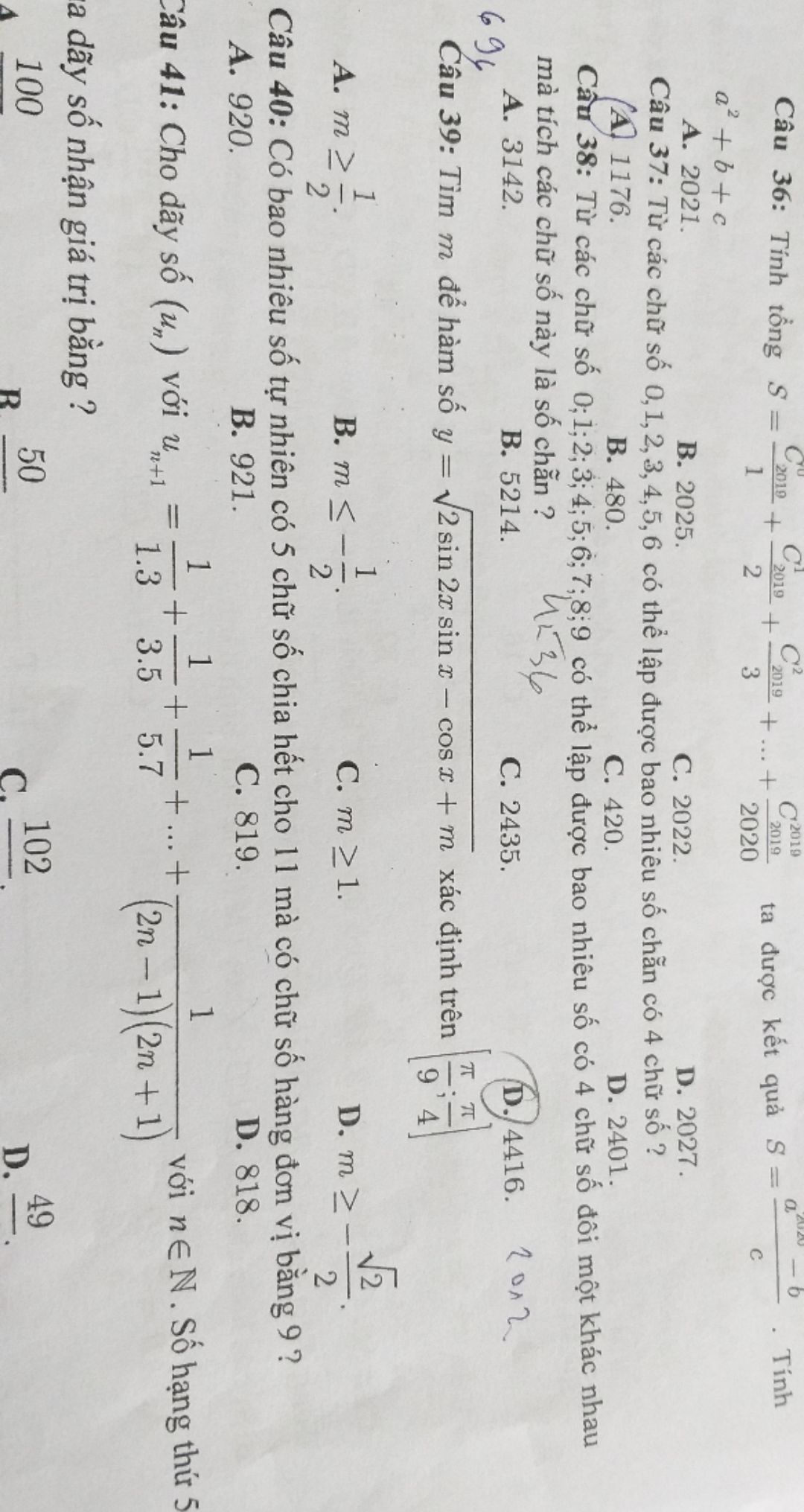 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Có bao nhiêu phương án trả lời của bài thi biết bài thi học kì môn Toán có 50 câu trắc nghiệm khách quan?
bởi Nấm Bé
 30/12/2019
Bài thi học kì môn Toán có 50 câu trắc nghiệm khách quan mỗi câu có bốn phương án trả lời Hỏi có bao nhiêu phương án trả lời của bài thiTheo dõi (1) 2 Trả lời
30/12/2019
Bài thi học kì môn Toán có 50 câu trắc nghiệm khách quan mỗi câu có bốn phương án trả lời Hỏi có bao nhiêu phương án trả lời của bài thiTheo dõi (1) 2 Trả lời -


Có bao nhiêu số tự nhiên có 6 chữ số khác nhau từng đôi một, trong đó 5 liền giữa 1 và 4?
bởi Thanh Dung
 30/12/2019
có bao nhiêu số tự nhiên có 6 chữ số khác nhau từng đôi một, trong đó 5 liền giữa 1 và 4Theo dõi (0) 0 Trả lời
30/12/2019
có bao nhiêu số tự nhiên có 6 chữ số khác nhau từng đôi một, trong đó 5 liền giữa 1 và 4Theo dõi (0) 0 Trả lời -

 So cách 5 người vào một băng ghế 7 chỗ làTheo dõi (0) 8 Trả lời
So cách 5 người vào một băng ghế 7 chỗ làTheo dõi (0) 8 Trả lời -


Với các chữ số 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau?
bởi Thùy Dung
 24/12/2019
24/12/2019
 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời
Bài tập SGK khác
Bài tập 2.22 trang 76 SBT Toán 11
Bài tập 2.23 trang 76 SBT Toán 11
Bài tập 2.25 trang 77 SBT Toán 11
Bài tập 2.26 trang 77 SBT Toán 10
Bài tập 2.27 trang 77 SBT Toán 10
Bài tập 2.28 trang 77 SBT Toán 11
Bài tập 2.29 trang 77 SBT Toán 11
Bài tập 2.30 trang 77 SBT Toán 11
Bài tập 2.31 trang 77 SBT Toán 11
Bài tập 5 trang 62 SGK Toán 11 NC
Bài tập 6 trang 62 SGK Toán 11 NC
Bài tập 7 trang 62 SGK Toán 11 NC
Bài tập 8 trang 62 SGK Toán 11 NC
Bài tập 9 trang 63 SGK Toán 11 NC
Bài tập 10 trang 63 SGK Toán 11 NC
Bài tập 11 trang 63 SGK Toán 11 NC
Bài tập 12 trang 63 SGK Toán 11 NC
Bài tập 13 trang 63 SGK Toán 11 NC
Bài tập 14 trang 63 SGK Toán 11 NC





