Giải bài 6 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1
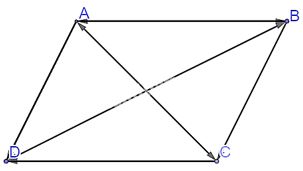
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \)
B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)
C. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {CD} \)
D. \(\overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {CD} \)
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
Quy tắc hình bình hành:
Cho hình bình hành ABCD, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Nghĩa là: Tổng hai vectơ cạnh chung điểm đầu của một hình bình hành bằng vectơ đường chéo có cùng điểm đầu đó.
Lời giải chi tiết
Áp dụng quy tắc và tính chất của hình bình hành ta có
\(\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) = \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {BC} \)
Chọn A
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST