Giải bài 6.55 trang 26 SBT Toán 10 Kết nối tri thức tập 2
Cho hàm số : \(y = \left\{ \begin{array}{l}2x + 3, - 2 \le x < - 1\\\frac{1}{2}x + \frac{3}{2}, - 1 \le x < 1\\ - \frac{1}{2}x + \frac{9}{2},1 \le x \le 3\end{array} \right.\)
a) Tìm tập xác định của hàm số
b) Vẽ đồ thị hàm số
c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số
d) Tìm tập giá trị của hàm số
Hướng dẫn giải chi tiết Bài 6.55
Phương pháp giải
Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D gọi là tập xác định của hàm số.
Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.
Lời giải chi tiết
a) Ta có: Hàm số xác định khi \({ - 2 \le x < - 1}\), \({ - 1 \le x < 1}\) và \({1 \le x \le 3}\) hay \(x \in [ - 2; - 1) \cup [ - 1;1) \cup [1;3]\)
=> tập xác định là \([ - 2; - 1) \cup [ - 1;1) \cup [1;3] = [-2 ; 3]\)
b) Đồ thị:
+ Vẽ đường thẳng \(y=2x+3\), giữ lại đường thẳng với \({ - 2 \le x < - 1}\) và bỏ phần còn lại.
+ Vẽ đường thẳng \(y=\frac{1}{2}x + \frac{3}{2}\), giữ lại đường thẳng với \({ - 2 \le x < - 1}\) và bỏ phần còn lại.
+ Vẽ đường thẳng \(y=-\frac{1}{2}x + \frac{9}{2}\), giữ lại đường thẳng với \({ 1 \le x \le 3}\) và bỏ phần còn lại.
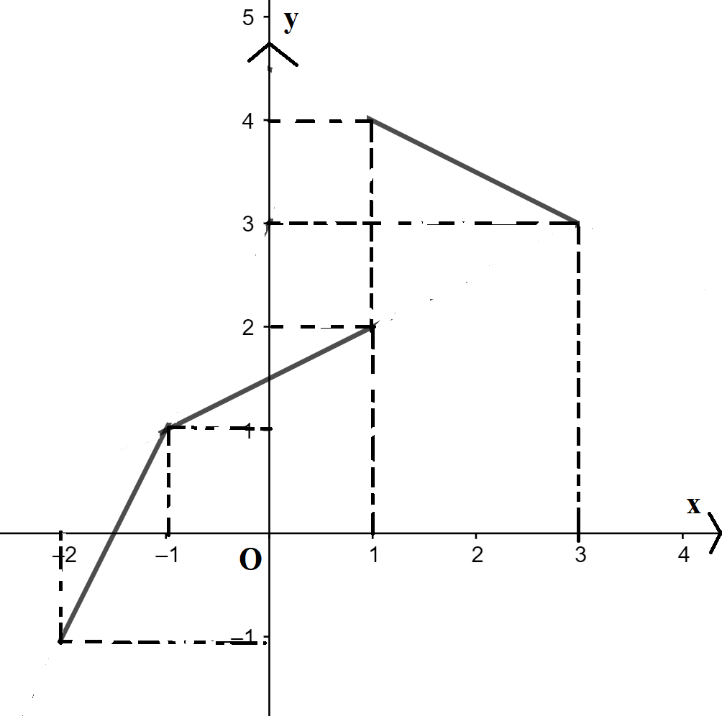
c) Quan sát từ trái sang phải:
+ Đồ thị hàm số đi lên trên khoảng (-2;-1) và (-1;2)
=> Hàm số đồng biến trên (-2 ; 1)
+ Đồ thị đi xuống trên (1;3) => Hàm số nghịch biến trên (1 ; 3)
d) Quang sát đồ thị,
+ với x thuộc [-2;1) thì giá trị của y thuộc [-1;2)
+ với x thuộc [1;3] thì giá trị của y thuộc [3;4]
=> Tập giá trị của hàm số là \([-1; 2) \cup {[3;4]}\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 6.53 trang 25 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.54 trang 25 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.56 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.57 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.58 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.59 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.60 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.61 trang 27 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.62 trang 27 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.63 trang 27 SBT Toán 10 Kết nối tri thức tập 2 - KNTT





