Giải bài 6.62 trang 27 SBT Toán 10 Kết nối tri thức tập 2
Trong Vật lí ta biết rằng, khi một vật được ném xiên với vận tốc ban đầu v0, góc ném hợp với phương ngang Ox một góc \(\alpha \), nếu ta bỏ qua sức cản của không khí và gió, vật chỉ chịu tác dụng của trọng lực với gia tốc trọng trường \(g \approx 9,8\) m/s2, thì độ cao y (so với mặt đất) của vật phụ thuộc vào khoảng cách theo phương ngang x (tính đến mặt đất tại điểm ném) theo một hàm số bậc hai cho bởi công thức
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \)
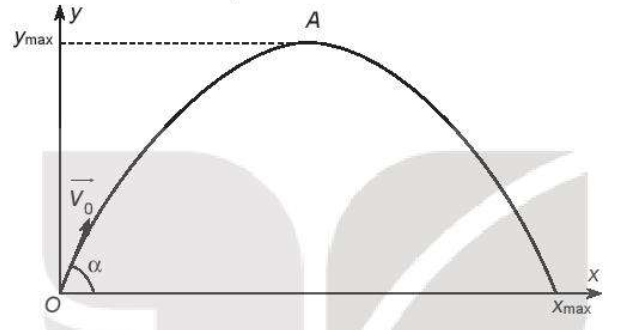
Như vậy quỹ đạo chuyển động của vật là một phần của đường parabol. Hãy xác định
a) Các hệ số a, b và c của hàm số bậc hai này
b) Độ cao lớn nhất mà vật có thể đạt được
c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném \(\alpha \) để độ cao của vật đạt giá trị lớn nhất
d) Một quả bóng được đá từ mặt đất lên cao với vận tốc ban đầu v0 = 20 m/s và góc đá so với phương ngang là 450. Khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng nào (làm tròn kết quả đến hàng phần trăm)?
Hướng dẫn giải chi tiết Bài 6.62
Phương pháp giải
Bước 1: Xác định các hệ số a, b, c dựa vào hàm số \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \)
Bước 2: Xác định tung độ đỉnh parabol là độ cao lớn nhất của vật
Bước 3: Tìm giá trị của \(\alpha \) để biểu thức \(\frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\) đạt GTLN
Bước 4: Thay các giá trị v0 = 20, \(\alpha = {45^0}\), \(g = 9,8\) để tìm dạng của hàm số
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \)
Bước 5: Cho y = 5, giải BPT y > 5 tìm ra khoảng của x là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng
Lời giải chi tiết
a) Hàm số bậc hai \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) có các hệ số:
\(a = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }} < 0\); \(b = \tan \alpha \); c = 0
b) Tam thức bậc hai \(\frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) có \(\Delta = {\tan ^2}\alpha \)
\( \Rightarrow \) Tung độ đỉnh của parabol là \( - \frac{\Delta }{{4a}} = \frac{{{{\tan }^2}\alpha }}{{\frac{{4g}}{{2v_0^2{{\cos }^2}\alpha }}}} = \frac{{v_0^2{{\tan }^2}\alpha .{{\cos }^2}\alpha }}{{2g}} = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\)
Vậy độ cao lớn nhất mà vật có thể đạt được là \(\frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\) m
c) \(\frac{{v_0^2{{\sin }^2}\alpha }}{{2g}} \le \frac{{v_0^2}}{{2g}}\) \( \Rightarrow {y_{\max }} = \frac{{v_0^2}}{{2g}}\) khi \(\sin \alpha = 1 \Leftrightarrow \alpha = {90^0}\)
Vậy với góc ném \(\alpha = {90^0}\) thì độ cao của vật đạt GTLN
d) Với v0 = 20 m/s, \(\alpha = {45^0}\), \(g = 9,8\) m/s2 ta có:
\(y = \frac{{ - 9,8}}{{{{2.20}^2}.{{\cos }^2}{{45}^0}}}{x^2} + x.\tan {45^0} \Leftrightarrow y = - \frac{{49}}{{2000}}{x^2} + x\)
Theo giả thiết, \(y > 5 \Leftrightarrow - \frac{{49}}{{2000}}{x^2} + x - 5 > 0 \Leftrightarrow 5,83 < x < 34,98\)
Vậy khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng \(x \in (5,83;34,98)\) mét.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





