Giải bài 6.59 trang 26 SBT Toán 10 Kết nối tri thức tập 2 - KNTT

Phương pháp giải

+ Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau:

1. Xác định toạ độ đính \(I\left( { - \frac{b}{{2{\rm{a}}}}; - \frac{\Delta }{{4{\rm{a}}}}} \right)\);

2. Vẽ trục đối xứng \({x =  - \frac{b}{{2{\rm{a}}}}}\);

3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol;

4. Vẽ parabol.

Lời giải chi tiết

a)

Đồ thị hàm số y = x² – 3x + 2 là parabol có bề lõm hướng lên, đỉnh là (1,5; –0,25), đi qua hai điểm (1; 0) và (2; 0). Đồ thị hàm số như hình vẽ:

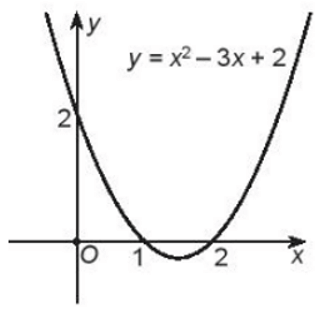
Việc giải bất phương trình x² – 3x + 2 ≥ 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía trên trục hoành. Từ đồ thị trên ta thấy khi x ≤ 1 và x ≥ 2 thì đồ thị hàm số y = x² – 3x + 2 nằm phía trên trục hoành.

Vậy tập nghiệm của bất phương trình là (–∞; 1]∪[2; +∞).

b)

Đồ thị hàm số y = x² – x – 6 là parabol có bề lõm hướng lên, đỉnh là: (0,5; –6,25), đi qua hai điểm (–2; 0), (3; 0) được vẽ trong hình sau:

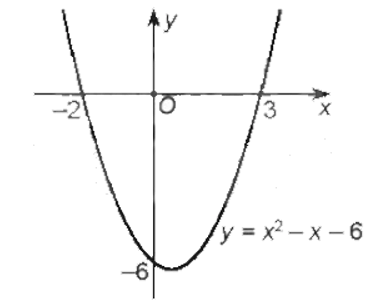
Việc giải bất phương trình y = x² – x – 6 < 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía dưới trục hoành. Từ đồ thị trên ta thấy khi –2 < x < 3 thì đồ thị hàm số y = x² – x – 6 nằm phía dưới trục hoành.

Vậy tập nghiệm của bất phương trình là (–2; 3). 

-- Mod Toán 10 HỌC247