Giải bài 4.19 trang 54 SBT Toán 10 Kết nối tri thức tập 1
Cho tam giác \(ABC.\)
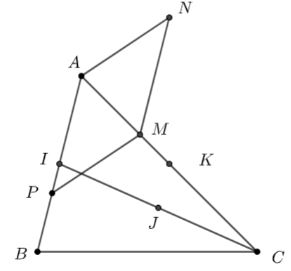
a) Tìm điểm \(M\) sao cho \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
b) Xác định điểm \(N\) thỏa mãn \(4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
Hướng dẫn giải chi tiết Bài 4.19
Phương pháp giải
a) Chứng minh \(M \equiv J\)
b) Gọi \(K\) là trung điểm của \(AC\).
Lấy điểm \(P\) thuộc cạnh \(AB\) sao cho \(\overrightarrow {AP} = \frac{2}{3}\overrightarrow {AB} \)
Chứng minh \(\overrightarrow {NM} = \overrightarrow {AP} \)
Lời giải chi tiết
a) Giả sử tìm được điểm \(M\) sao cho \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
Gọi \(I\) là trung điểm của \(AB\) và \(J\) là trung điểm của cạnh \(CI\).
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \;\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {MI} + \overrightarrow {IB} + 2\overrightarrow {MC} = 2\overrightarrow {MI} + 2\overrightarrow {MC} = 4\overrightarrow {MJ} \)
Mặt khác \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Rightarrow \) \(4\overrightarrow {MJ} = \overrightarrow 0 \,\, \Rightarrow \,\,\overrightarrow {MJ} = \overrightarrow 0 \,\, \Rightarrow \,\,M \equiv J\)
Vậy \(M\) là trung điểm của \(CI\).
b) Giả sử tìm được điểm \(N\) thỏa mãn \(4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
Gọi \(K\) là trung điểm của \(AC\).
Ta có: \(4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = 2\left( {\overrightarrow {NA} - \overrightarrow {NB} } \right) + \left( {\overrightarrow {NA} + \overrightarrow {NC} } \right) + \overrightarrow {NA} \)
\(\begin{array}{l} = 2\overrightarrow {BA} + \left( {\overrightarrow {NK} + \overrightarrow {KB} + \overrightarrow {NK} + \overrightarrow {KC} } \right) + \overrightarrow {NA} \\ = 2\overrightarrow {BA} + 2\overrightarrow {NK} + \overrightarrow {NA} \end{array}\)
Gọi \(M\) là điểm thỏa mãn \(2\overrightarrow {MK} + \overrightarrow {MA} = 0\)
Khi đó: \(2\overrightarrow {NK} + \overrightarrow {NA} = 2\left( {\overrightarrow {NM} + \overrightarrow {MK} } \right) + \overrightarrow {NM} + \overrightarrow {MA} = 3\overrightarrow {NM} \)
Do đó \(4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = 2\overrightarrow {BA} + 3\overrightarrow {NM} \)
Mặt khác \(4\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
\( \Rightarrow \) \(2\overrightarrow {BA} + 3\overrightarrow {NM} = \overrightarrow 0 \) \( \Leftrightarrow \) \(\overrightarrow {NM} = \frac{2}{3}\overrightarrow {AB} \) (1)
Lấy điểm \(P\) thuộc cạnh \(AB\) sao cho \(\overrightarrow {AP} = \frac{2}{3}\overrightarrow {AB} \) (2)
Từ (1) và (2) \( \Rightarrow \) \(\overrightarrow {NM} = \overrightarrow {AP} \)
\( \Rightarrow \) tứ giác \(APMN\) là hình bình hành
Vậy điểm \(N\) cần tìm là đỉnh thứ tư của hình bình hành \(APMN\).
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.