Giải bài 15 trang 47 SBT Toán 10 Cánh diều tập 1
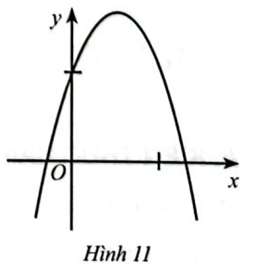
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị ở Hình 11. Xác định dấu \(a,b,c\)
Hướng dẫn giải chi tiết Bài 15
Phương pháp giải
Ta có parabol \(y = a{x^2} + bx + c\) có đỉnh \(\left( {\frac{{ - b}}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) và trục đối xứng của đường thẳng \(x = - \frac{b}{{2a}}\)
Lời giải chi tiết
+ Parabol có bề lõm hướng xuống dưới \( \Rightarrow a < 0\)
+ Parabol cắt trục tung tại điểm (0;c) nằm phía trên trục hoành nên \(c > 0\)
+ Đỉnh nằm bên phải trục tung nên có hoành độ dương hay \(x = \frac{{ - b}}{{2a}} > 0\), mà \(a < 0 \Rightarrow b > 0\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





