Giải bài 18 trang 48 SBT Toán 10 Cánh diều tập 1
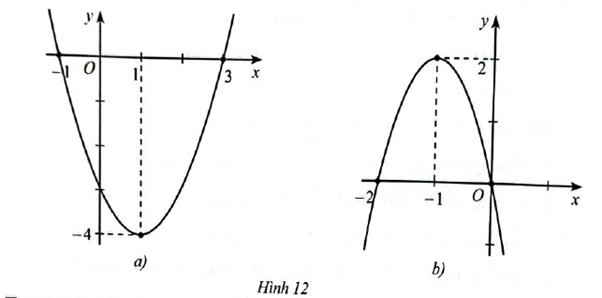
Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:
Hướng dẫn giải chi tiết Bài 18
Phương pháp giải
Xác định các hệ số a, b, c qua các đỉnh và các điểm thuộc parabol trong đồ thị đã cho
Lời giải chi tiết
Gọi hàm số bậc hai cần tìm là \(y = f\left( x \right) = a{x^2} + bx + c\)
a) Đồ thị hàm số có đỉnh là \(I\left( {1; - 4} \right)\) và đi qua điểm \(\left( { - 1;0} \right),\left( {3;0} \right)\), suy ra:\(\left\{ \begin{array}{l}x = \frac{{ - b}}{{2a}} = 1\\a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c = 0\\a{.3^2} + b.3 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a - b + c = 0\\9a + 3b + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = - 3\end{array} \right.\)
Vậy parabol đó là \(y = {x^2} - 2x - 3\)
b) Đồ thị hàm số có đỉnh là \(I\left( { - 1;2} \right)\) và đi qua điểm \(\left( {0;0} \right),\left( { - 2;0} \right)\), suy ra:\(\left\{ \begin{array}{l}x = \frac{{ - b}}{{2a}} = - 1\\a{.0^2} + b.0 + c = 0\\a.{\left( { - 2} \right)^2} + b.\left( { - 2} \right) + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 2a\\c = 0\\4a - 2b + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = - 4\\c = 0\end{array} \right.\)
Vậy parabol đó là \(y = - 2{x^2} - 4x\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





