Giải bài 14 trang 47 SBT Toán 10 Cánh diều tập 1 - CD

Phương pháp giải

Xác định đỉnh của parabol \(y = a{x^2} + bx + c\): \(\left( {\frac{{ - b}}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) và trục đối xứng của đường thẳng \(x =  - \frac{b}{{2a}}\)

Lời giải chi tiết

a) Hàm số \(y = 3{x^2} - 4x + 2\) có \(a = 3;b =  - 4;c = 2\)

+ Tọa độ đỉnh \(I\left( {\frac{{ - \left( { - 4} \right)}}{{2.3}}; - \frac{{{{\left( { - 4} \right)}^2} - 4.3.2}}{{4.3}}} \right) = \left( {\frac{2}{3};\frac{2}{3}} \right)\)

+ Trục đối xứng \(x = \frac{2}{3}\)

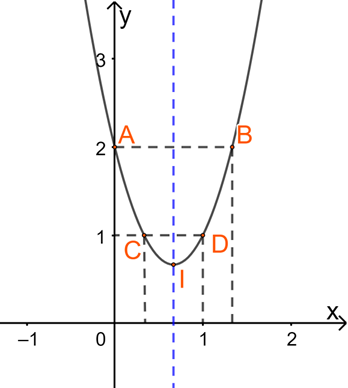
+ Giao điểm của parabol với trục tung là A(0;2).

+ Đồ thị hàm số không cắt trục hoành.

+ Điểm đối xứng với A(0;2) qua trục đối xứng \(x = \frac{2}{3}\) là \(B\left( {\frac{4}{3};2} \right)\)

+ Lấy \(C\left( {\frac{1}{3};1} \right)\) và \(D(1;1)\)

Từ đó ta có đồ thị hàm số:

b) Hàm số \(y =  - 2{x^2} - 2x - 1\) có \(a =  - 2;b =  - 2;c =  - 1\)

+ Đỉnh của parabol là \(I\left( {\frac{{ - \left( { - 2} \right)}}{{2.\left( { - 2} \right)}}; - \frac{{{{\left( { - 2} \right)}^2} - 4.\left( { - 2} \right).\left( { - 1} \right)}}{{4.\left( { - 2} \right)}}} \right) = \left( {\frac{{ - 1}}{2};\frac{{ - 1}}{2}} \right)\)

+ Trục đối xứng của hàm số là đường thẳng \(x = \frac{{ - 1}}{2}\)

+ Giao điểm của parabol với trục tung là A(0;-1).

+ Đồ thị hàm số không cắt trục hoành.

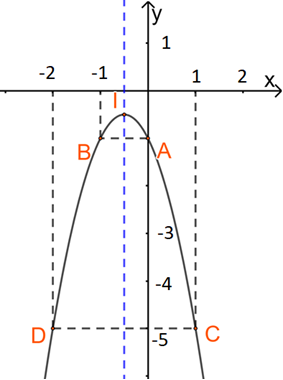
+ Điểm đối xứng với A(0;-1) qua trục đối xứng \(x = \frac{{ - 1}}{2}\) là \(B\left( { - 1; - 1} \right)\)

+ Lấy \(C\left( {1; - 5} \right)\) và \(D( - 2; - 5)\)

Từ đó ta có đồ thị hàm số:

-- Mod Toán 10 HỌC247