HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 8 B├Āi 25 Nhß╗ŗ thß╗®c Newton gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 72 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
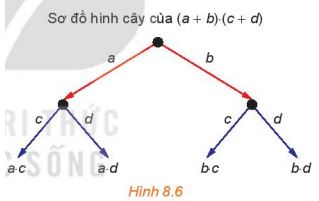
H├Ży x├óy dß╗▒ng sŲĪ ─æß╗ō h├¼nh c├óy cß╗¦a t├Łch hai nhß╗ŗ thß╗®c (a+b).(c+d) nhŲ░ sau:
- Tß╗½ mß╗Öt ─æiß╗ām gß╗æc, kß║╗ c├Īc m┼®i t├¬n, mß╗Śi m├╝i t├¬n tŲ░ŲĪng ß╗®ng vß╗øi mß╗Öt ─æŲĪn thß╗®c (gß╗Źi l├Ā nh├Żn cß╗¦a m┼®i t├¬n) cß╗¦a nhß╗ŗ thß╗®c thß╗® nhß║źt (H.8.6);
- Tß╗½ ngß╗Źn cß╗¦a mß╗Śi m┼®i t├¬n ─æ├Ż x├óy dß╗▒ng, kß║╗ c├Īc m┼®i t├¬n, mß╗Śi m├╝i t├¬n tŲ░ŲĪng ß╗®ng vß╗øi mß╗Öt ─æŲĪn thß╗®c cß╗¦a nhß╗ŗ thß╗®c thß╗® hai;
- Tß║Īi ngß╗Źn cß╗¦a c├Īc m┼®i t├¬n x├óy dß╗▒ng tß║Īi bŲ░ß╗øc sau c├╣ng, ghi lß║Īi t├Łch cß╗¦a c├Īc nh├Ż╠ēn cß╗¦a c├Īc m┼®i t├¬n ─æi tß╗½ ─æiß╗ām gß╗æc ─æß║┐n ─æß║¦u m├║t ─æ├│.
H├Ży lß║źy tß╗Ģng cß╗¦a c├Īc t├Łch nhß║Łn ─æŲ░ß╗Żc v├Ā so s├Īnh kß║┐t quß║Ż vß╗øi khai triß╗ān cß╗¦a t├Łch (a+b).(c+d)
-
Hoß║Īt ─æß╗Öng 2 trang 72 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
H├Ży cho biß║┐t c├Īc ─æŲĪn thß╗®c c├▓n thiß║┐u (...) trong sŲĪ ─æß╗ō h├¼nh c├óy (H.8.7) cß╗¦a t├Łch (a +b).(a +b).(a +b)
C├│ bao nhi├¬u t├Łch nhß║Łn ─æŲ░ß╗Żc lß║¦n lŲ░ß╗Żt bß║▒ng a3, a2b, ab2, b3?
H├Ży so s├Īnh ch├║ng vß╗øi c├Īc hß╗ć sß╗æ nhß║Łn ─æŲ░ß╗Żc khi khai triß╗ān (a + b)3.
-
Hoß║Īt ─æß╗Öng 3 trang 73 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
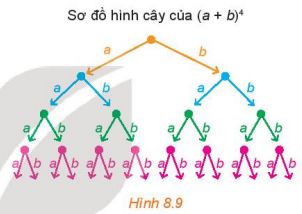
SŲĪ ─æß╗ō h├¼nh c├óy cß╗¦a khai triß╗ān (a + b)4 ─æŲ░ß╗Żc m├┤ tß║Ż nhŲ░ H├¼nh 8.9. Sau khi khai triß╗ān, ta thu ─æŲ░ß╗Żc mß╗Öt tß╗Ģng gß╗ōm 24 (theo quy tß║»c nh├ón) ─æŲĪn thß╗®c c├│ dß║Īng x.y.z.t, trong ─æ├│ mß╗Śi x, y, z, t l├Ā a hoß║Ęc b. Chß║│ng hß║Īn, nß║┐u x, y, t l├Ā a, c├▓n z l├Ā b th├¼ ta c├│ ─æŲĪn thß╗®c a.a.b.a, thu gß╗Źn l├Ā a3b. ─Éß╗ā c├│ ─æŲĪn thß╗®c n├Āy, th├¼ trong 4 nh├ón tß╗Ł x, y, z, t c├│ 1 nh├ón tß╗Ł l├Ā b, 3 nh├ón tß╗Ł c├▓n lß║Īi l├Ā a. Khi ─æ├│ sß╗æ ─æŲĪn thß╗®c ─æß╗ōng dß║Īng vß╗øi 3b trong tß╗Ģng l├Ā $C_{4}^{1}$.
Lß║Łp luß║Łn tŲ░ŲĪng tß╗▒ tr├¬n, d├╣ng kiß║┐n thß╗®c vß╗ü tß╗Ģ hß╗Żp, h├Ż╠āy cho biß║┐t trong tß╗Ģng n├¬u tr├¬n, c├│ bao nhi├¬u ─æŲĪn thß╗®c ─æß╗ōng dß║Īng vß╗øi mß╗Śi ─æŲĪn thß╗®c thu gß╗Źn sau:
+) a4 +) a3b +) a2b2 +) ab3 +) b4
-
Luyß╗ćn tß║Łp 1 trang 73 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khai triß╗ān \({\left( {x - 2} \right)^4}\).
-
Hoß║Īt ─æß╗Öng 4 trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
TŲ░ŲĪng tß╗▒ nhŲ░ H─É 3, sau khi khai triß╗ān (a + b)5, ta thu ─æŲ░ß╗Żc mß╗Öt tß╗Ģng gß╗ōm 25 ─æŲĪn thß╗®c c├│ dß║Īng x.y.z.t.u, trong ─æ├│ mß╗Śi k├Ł hiß╗ću x, y, z, t, u l├Ā a hoß║Ęc b. Chß║│ng hß║Īn, nß║┐u x, z l├Ā a, c├▓n y, t, u l├Ā b th├¼ ta c├│ ─æŲĪn thß╗®c a.b.a.b.b, thu gß╗Źn l├Ā a2b3. ─Éß╗ā c├│ ─æŲĪn thß╗®c n├Āy, th├¼ trong 5 nh├ón tß╗Ł x, y, x, t, u c├│ 3 nh├ón tß╗Ł l├Ā b, 2 nh├ón tß╗Ł c├▓n lß║Īi l├Ā a. Khi ─æ├│ sß╗æ ─æŲĪn thß╗®c ─æß╗ōng dß║Īng vß╗øi a2b3 trong tß╗Ģng l├Ā \(C_{5}^{3}\).
Lß║Łp luß║Łn tŲ░ŲĪng tß╗▒ nhŲ░ tr├¬n, d├╣ng kiß║┐n thß╗®c vß╗ü tß╗Ģ hß╗Żp, h├Ży cho biß║┐t, trong tß╗Ģng nhß║Łn ─æŲ░ß╗Żc n├¬u tr├¬n c├│ bao nhi├¬u ─æŲĪn thß╗® c ─æß╗ōng dß║Īng vß╗øi mß╗Ģi ─æŲĪn thß╗®c thu gß╗Źn sau:
+) a5 +) a4b +) a3b +) a2b3 +) ab4 +) b5
-
Luyß╗ćn tß║Łp 2 trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khai triß╗ān \({\left( {3x - 2} \right)^5}\)
-
Vß║Łn dß╗źng trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
a) D├╣ng hai sß╗æ hß║Īng ─æß║¦u ti├¬n trong khai triß╗ān cß╗¦a (1 + 0,05)4 ─æß╗ā t├Łnh gi├Ī trß╗ŗ gß║¦n ─æ├║ng cß╗¦a 1,054.
b) D├╣ng m├Īy t├Łnh cß║¦m tay t├Łnh gi├Ī trß╗ŗ cß╗¦a 1,054 v├Ā t├Łnh sai sß╗æ tuyß╗ćt ─æß╗æi cß╗¦a gi├Ī trß╗ŗ gß║¦n ─æ├║ng nhß║Łn ─æŲ░ß╗Żc ß╗¤ c├óu a.
-
Giß║Żi b├Āi 8.12 trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khai triß╗ān c├Īc ─æa thß╗®c:
a) (x -3)4
b) (3x - 2y)4
c) (x+5)4 + (x - 5)4
d) (x - 2y)5
-
Giß║Żi b├Āi 8.13 trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
T├¼m hß╗ć sß╗æ cß╗¦a \({x^4}\) trong khai triß╗ān cß╗¦a \({\left( {3x - 1} \right)^5}\)
-
Giß║Żi b├Āi 8.14 trang 74 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Biß╗āu diß╗ģn \((3+\sqrt{2})^{5}-(3-\sqrt{2})^{5}\) dŲ░ß╗øi dß║Īng \(a+b\sqrt{2}\) vß╗øi a, b l├Ā c├Īc sß╗æ nguy├¬n.
-
Giß║Żi b├Āi 8.15 trang 75 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
a) D├╣ng hai sß╗æ hß║Īng ─æß║¦u ti├¬n trong khai triß╗ān cß╗¦a (1 + 0,02)5 ─æß╗ā t├Łnh gi├Ī trß╗ŗ gß║¦n ─æ├║ng cß╗¦a 1,025
b) D├╣ng m├Īy tinh cß║¦m tay t├Łnh gi├Ī trß╗ŗ cß╗¦a 1,025v├Ā t├Łnh sai sß╗æ tuyß╗ćt ─æß╗æi cß╗¦a gi├Ī trß╗ŗ gß║¦n ─æ├║ng nhß║Łn ─æŲ░ß╗Żc ß╗¤ c├óu a.
-
Giß║Żi b├Āi 8.16 trang 75 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Sß╗æ d├ón cß╗¦a mß╗Öt t├¼nh ß╗¤ thß╗Øi ─æiß╗ām hiß╗ćn tß║Īi l├Ā khoß║Żng 800 ngh├¼n ngŲ░ß╗Øi. Giß║Ż sß╗Ł rß║▒ng tß╗ē lß╗ć t─āng d├ón sß╗æ hß║▒ng n─ām cß╗¦a tß╗ēnh ─æ├│ l├Ā r%.
a) Viß║┐t c├┤ng thß╗®c t├Łnh sß╗æ d├ón cß╗¦a tß╗ēnh ─æ├│ sau 1 n─ām, sau 2 n─ām. Tß╗½ ─æ├│ suy ra c├┤ng thß╗®c t├Łnh sß╗æ d├ón cß╗¦a tß╗ēnh ─æ├│ sau 5 n─ām nß╗»a l├Ā \(P=800\left ( 1+\frac{r}{100} \right )^{5}\) (ngh├¼n ngŲ░ß╗Øi).
b) Vß╗øi r = 1,5%, d├╣ng hai sß╗æ hß║Īng ─æß║¦u trong khai triß╗ān cß╗¦a (1 + 0,015)5 h├Ży Ų░ß╗øc t├Łnh sß╗æ d├ón cß╗¦a tß╗ēnh ─æ├│ sau 5 n─ām nß╗»a (theo ─æŲĪn vß╗ŗ ngh├¼n ngŲ░ß╗Øi).
-
Giß║Żi b├Āi 8.13 trang 57 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khai triß╗ān c├Īc ─æa thß╗®c
a) \({(x - 2)^4}\);
b) \({(x + 2)^5}\);
c) \({(2x - 3y)^4}\);
d) \({(2x - y)^5}\).
-
Giß║Żi b├Āi 8.14 trang 57 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Trong khai triß╗ān cß╗¦a \({(5x - 2)^5}\), sß╗æ m┼® cß╗¦a x ─æŲ░ß╗Żc sß║»p xß║┐p theo l┼®y thß╗½a t─āng dß║¦n, h├Ży t├¼m hß║Īng tß╗Ł thß╗® hai.
-
Giß║Żi b├Āi 8.15 trang 57 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
H├Ży sß╗Ł dß╗źng ba sß╗æ hß║Īng ─æß║¦u ti├¬n trong khai triß╗ān cß╗¦a \({(1 + 0,03)^4}\) ─æß╗ā t├Łnh gi├Ī trß╗ŗ gß║¦n ─æ├║ng cß╗¦a \(1,{03^4}\). X├Īc ─æß╗ŗnh sai sß╗æ tuyß╗ćt ─æß╗æi.
-
Giß║Żi b├Āi 8.16 trang 57 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├Īc ─æß╗ŗnh hß║Īng tß╗Ł kh├┤ng chß╗®a x trong khai triß╗ān cß╗¦a \({\left( {x + \frac{2}{x}} \right)^4}\).
-
Giß║Żi b├Āi 8.17 trang 57 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Khai triß╗ān \({\left( {{z^2} + 1 + \frac{1}{z}} \right)^4}\)