Hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 7 Bài 1 Tọa độ của vectơ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 60 SGK Toán 10 Cánh diều tập 2 - CD
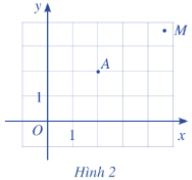
Trong mặt phẳng toạ độ Oxy (Hình 2), hãy:
a) Tìm hoành độ và tung độ của điểm A.
b) Nêu cách xác định toạ độ của điểm M tuỳ ý.
-
Hoạt động 2 trang 61 SGK Toán 10 Cánh diều tập 2 - CD
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vē vecto\(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.
-
Hoạt động 3 trang 61 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \).
-
Luyện tập 1 trang 62 SGK Toán 10 Cánh diều tập 2 - CD
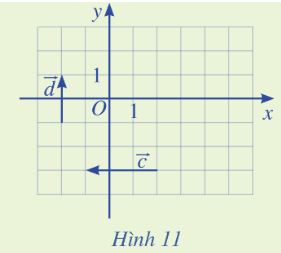
Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11
-
Hoạt động 4 trang 63 SGK Toán 10 Cánh diều tập 2 - CD
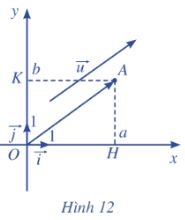
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\). Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \)
-
Luyện tập 2 trang 63 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\)
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \)
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \)
-
Hoạt động 5 trang 64 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho hai điểm A, B (Hình 13).
a) Tìm hoành độ\({x_A}\) , và tung độ\({y_A}\) , của điểm A; hoành độ \({x_B}\), và tung độ \({y_B}\) của điểm B.
b) Tìm điểm M sao cho\(\overrightarrow {OM} {\rm{ }} = {\rm{ }}\overrightarrow {AB} \) . Từ đó, tìm hoành độ a và tung độ b của vectơ\(\overrightarrow {AB} \) .
c) So sánh: \({x_B} - {x_A}\) và a; \({y_B} - {y_A}\) và b.
-
Luyện tập 3 trang 64 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1; 3) B(5; -1) C(2; -2) D(-2; 2)
Chứng minh : \(\overrightarrow {AB} = \overrightarrow {DC} \)
-
Giải bài 1 trang 65 SGK Toán 10 Cánh diều tập 2 - CD
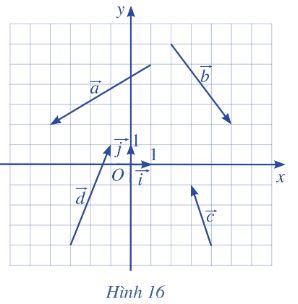
Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto \(\overrightarrow i , \overrightarrow j \)
-
Giải bài 2 trang 65 SGK Toán 10 Cánh diều tập 2 - CD
Tìm tọa độ của các vecto sau:
a) \(\overrightarrow a = 3\overrightarrow i \) b) \(\overrightarrow b = - \overrightarrow j \)
c) \(\overrightarrow c = \overrightarrow i - 4\overrightarrow j \) d) \(\overrightarrow d = 0,5\overrightarrow i + \sqrt 6 \overrightarrow j \)
-
Giải bài 3 trang 65 SGK Toán 10 Cánh diều tập 2 - CD
Tìm các cặp số thực a và b sao cho mỗi cặp vecto sau bằng nhau:
a) \(\overrightarrow u = \left( {2a - 1; - 3} \right)\) và \(\overrightarrow v = \left( {3;4b + 1} \right)\)
b) \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;4b} \right)\)
-
Giải bài 4 trang 66 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
a) Tìm toạ độ điểm M sao cho\(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) .
b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh\(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \) .
-
Giải bài 5 trang 66 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
-
Giải bài 6 trang 66 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(- 3 ; 1), B(-1; 3), I(4;2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.
-
Giải bài 7 trang 66 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1;- 2), N(4;- 1) và P(6 ; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm toạ độ của các điểm A, B, C.
-
Giải bài 1 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Toạ độ của vectơ \(\overrightarrow u = - 3\overrightarrow i + 2\overrightarrow j \) là:
A. \(( - 3;2)\)
B. \((2; - 3)\)
C. \(( - 3\overrightarrow i ;2\overrightarrow j )\)
D. \((3;2)\)
-
Giải bài 2 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Tọa độ của vectơ \(\overrightarrow u = 5\overrightarrow j \) là:
A. \((5;0)\)
B. \((5;\overrightarrow j )\)
C. \((0;5\overrightarrow j )\)
D. \((0;5)\)
-
Giải bài 3 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho A(2; −5). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. (2 ; 5)
B. (2; −5)
C. (−2; −5)
D. (−2; 5)
-
Giải bài 4 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho A(−1; 3), B(2; −1). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. (1; -4)
B. (-3; 4)
C. (3; -4)
D. (1; -2)
-
Giải bài 5 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow u = ( - 2; - 4),\overrightarrow v = (2x - y;y)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu:
A.\(\left\{ \begin{array}{l}x = 1\\y = - 4\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = - 3\\y = - 4\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 3\\y = 4\end{array} \right.\)
-
Giải bài 6 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Cho hình bình hành ABCD có A(–1 ; –2), B(3; 2), C(4; − 1). Toạ độ của đỉnh D là:
A. (8; 3)
B. (3; 8)
C. (-5; 0)
D. (0; -5)
-
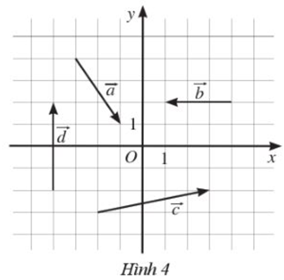
Giải bài 7 trang 61 SBT Toán 10 Cánh diều tập 2 - CD
Tìm toạ độ của các vectơ trong Hình 4.
-
Giải bài 8 trang 62 SBT Toán 10 Cánh diều tập 2 - CD
Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
a) \(\overrightarrow m = (2a + 3;b - 1)\) và \(\overrightarrow n = (1; - 2)\)
b) \(\overrightarrow u = (3a - 2;5)\)và \(\overrightarrow v = (5;2b + 1)\)
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b - 3a)\)
-
Giải bài 9 trang 62 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
-
Giải bài 10 trang 62 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho tứ giác ABCD có \(A({x_A};{y_A});B({x_B};{y_B});C({x_C};{y_C});D({x_D};{y_D})\). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \({x_A} + {x_C} = {x_B} + {x_D}\) và \({y_A} + {y_C} = {y_B} + {y_D}\)
-
Giải bài 11 trang 62 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng M(1 ; – 2), N(3 ; 1), P(− 1 ; 2). Tìm toạ độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.